题目内容
函数y=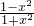 的值域是
的值域是
- A.[-1,1]
- B.(-1,1]
- C.[-1,1)
- D.(-1,1)
B
分析:进行变量分离y=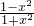 =
= -1,若令t=1+x2则可变形为y=
-1,若令t=1+x2则可变形为y=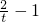 (t≥1)利用反比例函数图象求出函数的值域.
(t≥1)利用反比例函数图象求出函数的值域.
解答:解法一:y=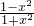 =
= -1.∵1+x2≥1,
-1.∵1+x2≥1,
∴0< ≤2.∴-1<y≤1.
≤2.∴-1<y≤1.
解法二:由y=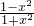 ,得x2=
,得x2=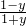 .
.
∵x2≥0,∴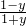 ≥0,解得-1<y≤1.
≥0,解得-1<y≤1.
故选B
点评:此类分式函数的值域通常采用逆求法、分离变量法,应注意理解并加以运用.
解法三:令x=tanθ(- <θ<
<θ< ),则y=
),则y= =cos2θ.
=cos2θ.
∵-π<2θ<π,
∴-1<cos2θ≤1,即-1<y≤1.
分析:进行变量分离y=
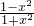 =
= -1,若令t=1+x2则可变形为y=
-1,若令t=1+x2则可变形为y=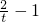 (t≥1)利用反比例函数图象求出函数的值域.
(t≥1)利用反比例函数图象求出函数的值域.解答:解法一:y=
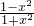 =
= -1.∵1+x2≥1,
-1.∵1+x2≥1,∴0<
 ≤2.∴-1<y≤1.
≤2.∴-1<y≤1.解法二:由y=
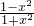 ,得x2=
,得x2=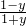 .
.∵x2≥0,∴
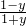 ≥0,解得-1<y≤1.
≥0,解得-1<y≤1.故选B
点评:此类分式函数的值域通常采用逆求法、分离变量法,应注意理解并加以运用.
解法三:令x=tanθ(-
 <θ<
<θ< ),则y=
),则y= =cos2θ.
=cos2θ.∵-π<2θ<π,
∴-1<cos2θ≤1,即-1<y≤1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的值域是
( )
的值域是
( ) 的值域是
( )
的值域是
( )