题目内容
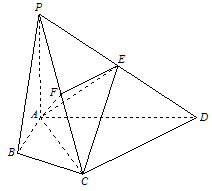
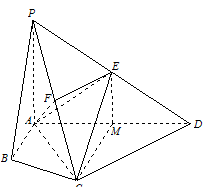
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅰ)解:在Rt△ABC中,AB=1,∠BAC=60°,
∴BC=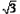 ,AC=2.
,AC=2.
在Rt△ACD中,AC=2,∠CAD=60°,
∴CD=2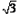 ,AD=4.
,AD=4.
∴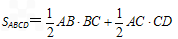
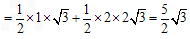
则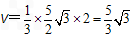
(Ⅱ)证明:∵PA=CA,F为PC的中点,
∴AF⊥PC.
∵PA⊥平面ABCD,
∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
∴CD⊥PC.
∵E为PD中点,F为PC中点,
∴EF∥CD.则EF⊥PC.
∵AF∩EF=F,
∴PC⊥平面AEF.
∴BC=
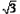 ,AC=2.
,AC=2.在Rt△ACD中,AC=2,∠CAD=60°,
∴CD=2
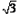 ,AD=4.
,AD=4.∴
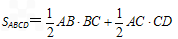
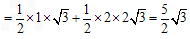
则
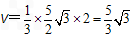
(Ⅱ)证明:∵PA=CA,F为PC的中点,
∴AF⊥PC.
∵PA⊥平面ABCD,
∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
∴CD⊥PC.
∵E为PD中点,F为PC中点,
∴EF∥CD.则EF⊥PC.
∵AF∩EF=F,
∴PC⊥平面AEF.


练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD, 如图.在四棱锥P一ABCD中,底面ABCD是正方形,侧棱PD⊥底 面ABCD,PD=DC=2,E是PC的中点.
如图.在四棱锥P一ABCD中,底面ABCD是正方形,侧棱PD⊥底 面ABCD,PD=DC=2,E是PC的中点. 已知在四棱锥P一ABCD中,二面角P一AD一B为60°,∠PDA=45°,∠DAB=90°,∠PAD=90°,∠ADC=135°,
已知在四棱锥P一ABCD中,二面角P一AD一B为60°,∠PDA=45°,∠DAB=90°,∠PAD=90°,∠ADC=135°, 如图,在四棱锥P一ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.PA=PD=AD=2,点M在线段PC上 PM=
如图,在四棱锥P一ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.PA=PD=AD=2,点M在线段PC上 PM= (本小题满分14分)在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD与底面ABCD垂直,PD=DC,E是PC的中点,作EF
(本小题满分14分)在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD与底面ABCD垂直,PD=DC,E是PC的中点,作EF