题目内容
设M是椭圆 上的任意一点,若F1,F2是椭圆的两个焦点,则|MF1|+|MF2|等于
上的任意一点,若F1,F2是椭圆的两个焦点,则|MF1|+|MF2|等于
- A.2
- B.3
- C.4
- D.6
D
分析:利用椭圆的概念即可求得|MF1|+|MF2|的值.
解答:∵M是椭圆 +
+ =1上的任意一点,
=1上的任意一点,
又F1,F2是椭圆的两个焦点,
∴|MF1|+|MF2|=2a=6.
故选D.
点评:本题考查椭圆的概念,属于基础题.
分析:利用椭圆的概念即可求得|MF1|+|MF2|的值.
解答:∵M是椭圆
 +
+ =1上的任意一点,
=1上的任意一点,又F1,F2是椭圆的两个焦点,
∴|MF1|+|MF2|=2a=6.
故选D.
点评:本题考查椭圆的概念,属于基础题.

练习册系列答案
相关题目
 (2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
(2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为 (2013•汕头一模)如图.已知椭圆
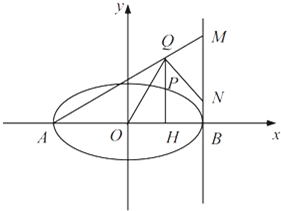
(2013•汕头一模)如图.已知椭圆