题目内容
9.(重点中学做)甲乙两个人参加射击训练,射击一次中靶的概率分别是p1,p2,其中$\frac{1}{{p}_{1}}$,$\frac{1}{{p}_{2}}$是函数f(x)=$\frac{1}{3}$x3-$\frac{5}{2}$x2+mx(x∈R)的两极值点,函数g(x)=sinx-2x+2在区间[0,2π]上的最大值为$\frac{1}{{p}_{1}}$.(1)求p1,p2的值;
(2)两人各射击1次,求两人中至少中靶1次的概率.
分析 (1)分别求得导数,由单调性可得最值,结合韦达定理,即可得到所求值;
(2)运用分类讨论和间接法,即可得到所求概率.
解答 解:(1)g(x)的导数为g′(x)=cosx-2<0,
即有g(x)在[0,2π]递减,可得g(x)max=g(0)=2,
$\frac{1}{{p}_{1}}$=2,可得p1=$\frac{1}{2}$,f′(x)=x2-5x+m,
令f′(x)=0,可得$\frac{1}{{p}_{1}}$+$\frac{1}{{p}_{2}}$=5,
解得p2=$\frac{1}{3}$;
(2)两人中至少中靶1次分两种情况:
①恰好中靶一次的概率为$\frac{1}{2}$×(1-$\frac{1}{3}$)+(1-$\frac{1}{2}$)×$\frac{1}{3}$=$\frac{1}{2}$,
②恰好中靶两次的概率为$\frac{1}{2}$×$\frac{1}{3}$=$\frac{1}{6}$,
则两人中至少中靶1次的概率为$\frac{1}{2}$+$\frac{1}{6}$=$\frac{2}{3}$.
或两人均未中靶的概率为(1-$\frac{1}{2}$)×(1-$\frac{1}{3}$)=$\frac{1}{3}$,
则两人中至少中靶1次的概率为1-$\frac{1}{3}$=$\frac{2}{3}$.
点评 本题考查导数的运用:求极值和最值,考查直接法和间接法求概率,属于基础题.

练习册系列答案
相关题目
19.已知正方体、等边圆柱(轴截面是正方形)、球的体积相等,它们的表面积分别为S正、S柱、S球,则( )
| A. | S正<S球<S柱 | B. | S正<S柱<S球 | C. | S球<S柱<S正 | D. | S球<S正<S柱 |
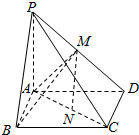 已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.
已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.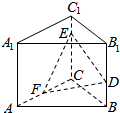 如图,已知正三棱柱ABC-A1B1C1中,AA1=4,AB=6,点D,E,F分别在棱BB1,CC1,AF上,且BD=C1E=$\frac{1}{2}$AF=1.
如图,已知正三棱柱ABC-A1B1C1中,AA1=4,AB=6,点D,E,F分别在棱BB1,CC1,AF上,且BD=C1E=$\frac{1}{2}$AF=1.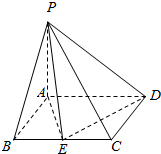 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E为棱BC的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E为棱BC的中点.