题目内容
已知函数f(x)=lnax- (a≠0).
(a≠0).(Ⅰ)讨论函数f(x)的单调区间;
(Ⅱ)当a=1时,是否存在过点(1,-1)的直线与函数y=f(x)的图象相切?若存在,有多少条?若不存在,说明理由.
【答案】分析:(Ⅰ)求导数,利用导数讨论函数f(x)的单调区间;
(Ⅱ)求导数,利用导数的几何意义进行判断.
解答:解析:(1)由题意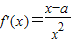 . …(1分)
. …(1分)
当a>0时,函数f(x)的定义域为(0,+∞),f'(x)>0,则x∈(a,+∞),f'(x)<0,则x∈(0,a),
此时函数在(0,a)上是减函数,在(a,+∞)上是增函数,…(3分)
当a<0时,函数f(x)的定义域为(-∞,0),f'(x)>0,则x∈(a,0),f'(x)<0,则x∈(-∞,a),
此时函数在(-∞,a)上是减函数,在(a,0)上是增函数.…(5分)
(2)假设存在这样的切线,设其中一个切点T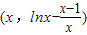 ,
,
∴切线方程: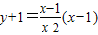 ,将点T坐标代入得:
,将点T坐标代入得:
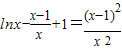 ,即
,即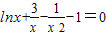 ,①
,①
设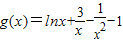 ,则
,则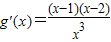 .
.
令g'(x)=0,则x=1或x=2.…(8分)
所以g(x)在区间(0,1),(2,+∞)上是增函数,在区间(1,2)上是减函数,g(x)在x=1处取得极大值g(1)=1,在x=2处取得极小值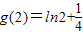 ,
,
所以g(x)>0在[1,+∞)上恒成立,即g(x)=0在[1,+∞)上无解.
因为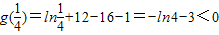 ,g(1)=1>0,g(x)在区间(0,1)上单调递增,
,g(1)=1>0,g(x)在区间(0,1)上单调递增,
根据零点定理,g(x)在区间(0,1)上有且仅有一个实数根,即方程①有且仅有一解,故符合条件的切线有且仅有一条.…(12分)
点评:本题主要考查利用导数研究函数的性质,要求熟练掌握导数和函数单调性,极值之间的关系,考查学生的运算能力.
(Ⅱ)求导数,利用导数的几何意义进行判断.
解答:解析:(1)由题意
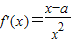 . …(1分)
. …(1分)当a>0时,函数f(x)的定义域为(0,+∞),f'(x)>0,则x∈(a,+∞),f'(x)<0,则x∈(0,a),
此时函数在(0,a)上是减函数,在(a,+∞)上是增函数,…(3分)
当a<0时,函数f(x)的定义域为(-∞,0),f'(x)>0,则x∈(a,0),f'(x)<0,则x∈(-∞,a),
此时函数在(-∞,a)上是减函数,在(a,0)上是增函数.…(5分)
(2)假设存在这样的切线,设其中一个切点T
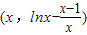 ,
,∴切线方程:
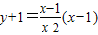 ,将点T坐标代入得:
,将点T坐标代入得: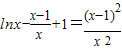 ,即
,即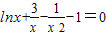 ,①
,①设
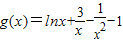 ,则
,则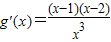 .
.令g'(x)=0,则x=1或x=2.…(8分)
| x | (0,1) | 1 | (1,2) | 2 | (2,+∞) |
| g'(x) | + | - | + | ||
| g(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
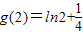 ,
,所以g(x)>0在[1,+∞)上恒成立,即g(x)=0在[1,+∞)上无解.
因为
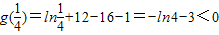 ,g(1)=1>0,g(x)在区间(0,1)上单调递增,
,g(1)=1>0,g(x)在区间(0,1)上单调递增,根据零点定理,g(x)在区间(0,1)上有且仅有一个实数根,即方程①有且仅有一解,故符合条件的切线有且仅有一条.…(12分)
点评:本题主要考查利用导数研究函数的性质,要求熟练掌握导数和函数单调性,极值之间的关系,考查学生的运算能力.

练习册系列答案
相关题目