题目内容
直线l是双曲线 -
- =1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为
=1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为
- A.2
- B.

- C.

- D.

A
分析:根据椭圆可得双曲线、圆与准线的结合图象,进而根据三角形与双曲线的有关性质顶点答案即可.
解答: 解:根据题意可得双曲线与圆的位置关系如图所示.
解:根据题意可得双曲线与圆的位置关系如图所示.
因为圆被双曲线的右准线l分成弧长为2:1的两段圆弧,
所以∠AOB=60°.
又因为圆是以原点为圆心且过双曲线的顶点,
所以OA=a,且B( ,0).
,0).
所以 ,
,
所以双曲线的离心率为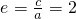 .
.
故选A.
点评:解决此类问题的关键是熟练掌握双曲线的有关性质,以及双曲线中有关数值的基本关系.
分析:根据椭圆可得双曲线、圆与准线的结合图象,进而根据三角形与双曲线的有关性质顶点答案即可.
解答:
 解:根据题意可得双曲线与圆的位置关系如图所示.
解:根据题意可得双曲线与圆的位置关系如图所示.因为圆被双曲线的右准线l分成弧长为2:1的两段圆弧,
所以∠AOB=60°.
又因为圆是以原点为圆心且过双曲线的顶点,
所以OA=a,且B(
 ,0).
,0).所以
 ,
,所以双曲线的离心率为
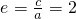 .
.故选A.
点评:解决此类问题的关键是熟练掌握双曲线的有关性质,以及双曲线中有关数值的基本关系.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 -
- =1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为( )
=1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为( )


 -
- =1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为( )
=1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为( )


 -
- =1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为( )
=1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为( )


 -
- =1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为( )
=1的右准线,以原点为圆心且过双曲线的顶点的圆,被直线l分成弧长为2:1的两段圆弧,则该双曲线的离心率为( )

