题目内容
已知a是实数,函数f(x)=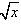 (x-a),
(x-a),
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设g(a)为f(x)在区间[0,2]上的最小值,
(ⅰ)写出g(a)的表达式;
(ⅱ)求a的取值范围,使得-6≤g(a)≤-2。
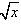 (x-a),
(x-a),(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设g(a)为f(x)在区间[0,2]上的最小值,
(ⅰ)写出g(a)的表达式;
(ⅱ)求a的取值范围,使得-6≤g(a)≤-2。
解:(Ⅰ)函数的定义域为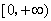 ,
,
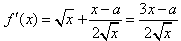 (x>0),
(x>0),
若a≤0,则f′(x)>0, f(x)有单调递增区间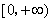 ;
;
若a>0,令f′(x)=0,得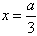 ,
,
当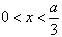 时,f′(x)<0,当
时,f′(x)<0,当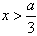 时,f′(x)>0,
时,f′(x)>0,
f(x)有单调递减区间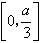 ,单调递增区间
,单调递增区间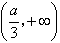 .
.
(Ⅱ)(i)若a≤0,f(x)在[0,2]上单调递增,所以g(a)=f(0)=0;
若0<a<6,f(x)在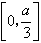 上单调递减,在
上单调递减,在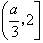 上单调递增,
上单调递增,
所以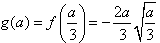 ;
;
若a≥6,f(x)在[0,2]上单调递减,所以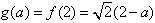 ;
;
综上所述,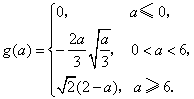 。
。
(ii)令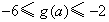 ,
,
若a≤0,无解;
若0<a<6,解得3≤a<6;
若a≥6,解得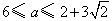 ;
;
故a的取值范围为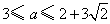 。
。
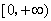 ,
,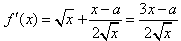 (x>0),
(x>0),若a≤0,则f′(x)>0, f(x)有单调递增区间
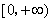 ;
;若a>0,令f′(x)=0,得
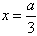 ,
,当
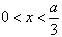 时,f′(x)<0,当
时,f′(x)<0,当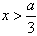 时,f′(x)>0,
时,f′(x)>0,f(x)有单调递减区间
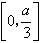 ,单调递增区间
,单调递增区间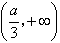 .
.(Ⅱ)(i)若a≤0,f(x)在[0,2]上单调递增,所以g(a)=f(0)=0;
若0<a<6,f(x)在
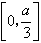 上单调递减,在
上单调递减,在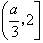 上单调递增,
上单调递增,所以
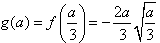 ;
;若a≥6,f(x)在[0,2]上单调递减,所以
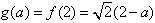 ;
;综上所述,
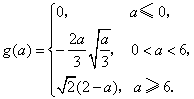 。
。(ii)令
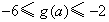 ,
,若a≤0,无解;
若0<a<6,解得3≤a<6;
若a≥6,解得
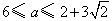 ;
;故a的取值范围为
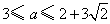 。
。
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目