Question

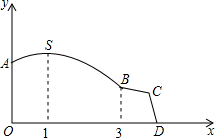安通驾校拟围着一座山修建一条环形训练道路OASBCD，道路的平面图如图所示（单位：km），已知曲线ASB为函数y=Asin（ωx+φ）（A＞0，0＜ω＜1，|φ|＜

π

2

），x∈[0，3]的图象，且最高点为S（1，2），折线段AOD为固定线路，其中AO=

3

，OD=4，折线段BCD为可变线路，但为保证驾驶安全，限定∠BCD=120°．
（1）求A，ω，φ的值；
（2）应如何设计，才能使折线段道路BCD最长？

Answer 1

分析：（1）根据最高点S的纵坐标确定出A的值，将A坐标代入求出sinφ的值，确定出φ的度数，将S坐标代入求出ω的值；
（2）将B的横坐标代入函数解析式求出纵坐标，确定出BD的长，在三角形BCD中，利用正弦定理列出关系式，表示出CD与BC，进而表示出BC+CD，整理为一个角的正弦函数，根据正弦函数的定义域与值域求出折线BCD的最大值，以及此时θ的值．

解答：解：（1）由已知最高点S（1，2），得到A=2，
且有2sinφ=

3

，即sinφ=

3

2

，
∵|?|＜

π

2

，∴φ=

π

3

，
又∵最高点为（1，2），
∴2sin（ω+

π

3

）=2，
解得：ω=

π

6

，
∴y=2sin（

π

6

x+

π

3

）；
（2）∵B点的横坐标为3，代入函数解析式得y_B=2sin（

π

6

×3+

π

3

）=1，
∴BD=

12+(4-3)2

=

2

，
在△BCD中，设∠CBD=θ，则∠BDC=180°-120°-θ=60°-θ．
由正弦定理有

BD

sin120°

=

CD

sinθ

=

BC

sin(60°-θ)

，
∴CD=

2 6

3

sinθ，BC=

2 6

3

sin（60°-θ），
∴BC+CD=

2 6

3

[sinθ+sin（60°-θ）]=

2 6

3

[sinθ+

3

2

cosθ-

1

2

sinθ]=

2 6

3

sin（θ+

π

3

），
∴当且仅当θ=

π

6

时，折线段BCD最长，最长为

2 6

3

千米．

点评：此题考查了两角和与差的正弦函数公式，以及正弦函数的单调性，熟练掌握公式是解本题的关键．