题目内容
设集合A={x|x2-2x-3＜0}，B={x|2x＞1}，则A∩B= ．
分析：求解一元二次不等式化简集合A，求解指数不等式化简集合B，然后直接利用交集运算求解．
解答：解：由集合A={x|x2-2x-3＜0}={x|-1＜x＜3}，B={x|2x＞1}={x|x＞0}，
则A∩B={x|-1＜x＜3}∩{x|x＞0}={x|0＜x＜3}．
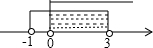
故答案为：{x|0＜x＜3}．
则A∩B={x|-1＜x＜3}∩{x|x＞0}={x|0＜x＜3}．
故答案为：{x|0＜x＜3}．
点评：本题考查了交集及其运算，考查了一元二次不等式及指数不等式的解法，是基础的计算题．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目