题目内容
已知数列{an}满足an+1=|an-1|(n∈N*).
(1)a1=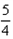 ,计算a2,a3,a4的值,并写出数列{an}(n∈N*,n≥2)的通项公式;
,计算a2,a3,a4的值,并写出数列{an}(n∈N*,n≥2)的通项公式;
(2) 是否存在a1,n0(a1∈R,n0∈N*),使得当n≥n0(n∈N*)时, an恒为常数,若存在,求出a1,n0,否则说明理由;
(3) 若a1=a∈(k,k+1),(k∈N*). ,求{an}的前3k项的和S3k(用k,a表示).
解(1)  ,
,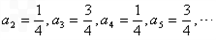 ,以此类推
,以此类推 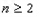 时,
时,  其中
其中 .
.
(2)∵
∴an≥1时,  .
.
若0<a1<1时, a2=1-a1,a3=1-a2=a1,此时只需 ,故存在
,故存在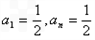 .
.
若a1=b≥1时,不妨设若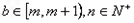 时,
时, 时,
时,  ,
,
∴
∴a1=m+ ,n≥m+1时,
,n≥m+1时, .
.
若a1=c<0,不妨设 ,
,
∴a2=-c+1∈(l,l+1),
∴a3=a2-1=-c,a4=-c-1,

 ,
, ,则
,则 .
.
故存在三组  和
和 :
: 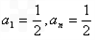 ;
;  ;
;  ;其中
;其中 
(3)  ,
, 时,
时, ,
, 
 .
. 


练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目