题目内容
在数列 中,对于任意
中,对于任意 ,等式
,等式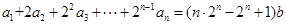 成立,其中常数
成立,其中常数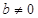 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求证:数列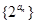 为等比数列;
为等比数列;
(Ⅲ)如果关于n的不等式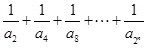
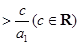 的解集为
的解集为 ,求b和c的取值范围.
,求b和c的取值范围.
【答案】
(Ⅰ)解:因为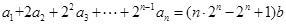 ,
,
所以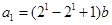 ,
,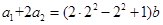 ,
,
解得 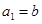 ,
,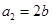 .
………………………… 3分
.
………………………… 3分
(Ⅱ)证明:当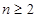 时,由
时,由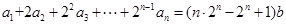 , ①
, ①
得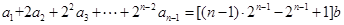 ,
②
,
②
将①,②两式相减,得 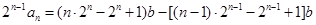 ,
,
化简,得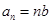 ,其中
,其中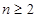 .
………………… 5分
.
………………… 5分
因为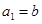 ,
,
所以 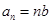 ,其中
,其中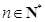 .
………………………… 6分
.
………………………… 6分
因为 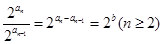 为常数,
为常数,
所以数列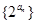 为等比数列. …………………… 8分
为等比数列. …………………… 8分
(Ⅲ)解:由(Ⅱ),得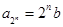 , ……………………… 9分
, ……………………… 9分
所以
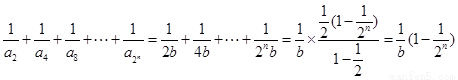 , 11分
, 11分
又因为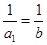 ,
,
所以不等式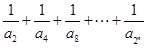
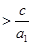 化简为
化简为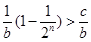 ,
,
当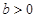 时,考察不等式
时,考察不等式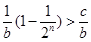 的解,
的解,
由题意,知不等式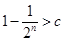 的解集为
的解集为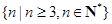 ,
,
因为函数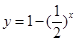 在R上单调递增,
在R上单调递增,
所以只要求 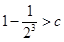 且
且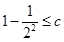 即可,
即可,
解得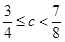 ; …………………… 13分
; …………………… 13分
当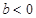 时,考察不等式
时,考察不等式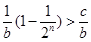 的解,
的解,
由题意,要求不等式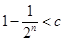 的解集为
的解集为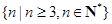 ,
,
因为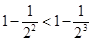 ,
,
所以如果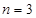 时不等式成立,那么
时不等式成立,那么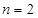 时不等式也成立,
时不等式也成立,
这与题意不符,舍去.
所以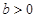 ,
,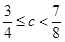 .
………………………… 14分
.
………………………… 14分
【解析】本试题主要是考查了数列通项公式的运用,以及数列与不等式的综合运用。
(1)因为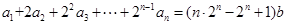 ,
,
所以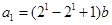 ,
,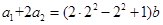 ,
,
解得 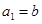 ,
,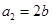 .
.
(2)采用整体的思想,作差法得到通项公式的表示,进而得到结论。
(3)由(Ⅱ),得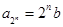 , ……………………… 9分
, ……………………… 9分
所以
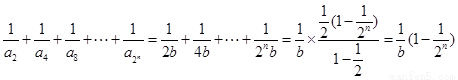
然后求和化简得到。

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
 中,对于任意
中,对于任意 ,等式:
,等式: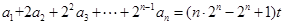 恒成立,其中常数
恒成立,其中常数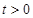 .
.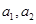 的值;
的值; 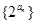 为等比数列;
为等比数列;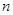 的不等式
的不等式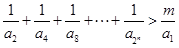 的解集为
的解集为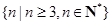 ,试求实数
,试求实数 的取值范围.
的取值范围.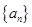 中,对于任意
中,对于任意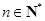 ,等式:
,等式: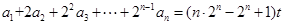 恒成立,其中常数
恒成立,其中常数 .
.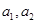 的值; (2)求证:数列
的值; (2)求证:数列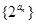 为等比数列;
为等比数列;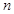 的不等式
的不等式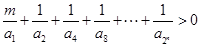 的解集为
的解集为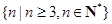 ,试求实数
,试求实数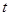 、
、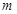 的取值范围.
的取值范围.