题目内容
(本题11分)已知圆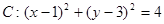 ,过原点
,过原点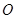 的直线
的直线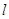 与圆
与圆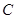 相交于
相交于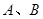 两点
两点
(1) 若弦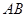 的长为
的长为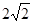 ,求直线
,求直线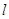 的方程;
的方程;
(2)求证: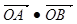 为定值。
为定值。
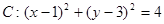 ,过原点
,过原点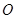 的直线
的直线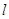 与圆
与圆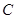 相交于
相交于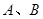 两点
两点(1) 若弦
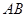 的长为
的长为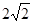 ,求直线
,求直线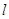 的方程;
的方程;(2)求证:
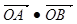 为定值。
为定值。(1)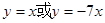 ;(2)当
;(2)当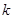 不存在时,直线为
不存在时,直线为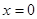 ,此时
,此时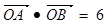 ,当
,当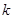 存在时,设直线
存在时,设直线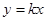 ,设
,设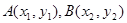 ,
,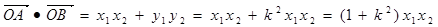
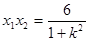 所以
所以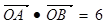 。
。
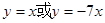 ;(2)当
;(2)当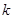 不存在时,直线为
不存在时,直线为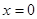 ,此时
,此时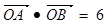 ,当
,当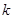 存在时,设直线
存在时,设直线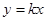 ,设
,设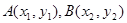 ,
,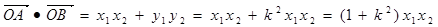
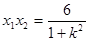 所以
所以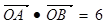 。
。 试题分析:(1)设直线方程
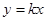 ,所以
,所以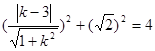 ,………3分
,………3分解得
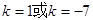
所以直线方程为
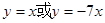 ……………………………5分
……………………………5分(2)当
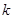 不存在时,直线为
不存在时,直线为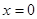 ,此时
,此时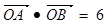 ……6分
……6分当
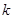 存在时,设直线
存在时,设直线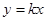 ,
,设
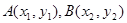 ,
,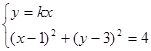 消y得
消y得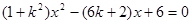 ,……7分
,……7分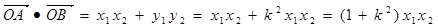
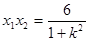 所以
所以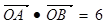
综上:
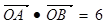 ……………………………11分
……………………………11分另法:
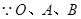 三点共线,
三点共线,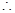
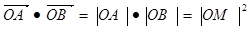 (
(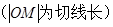 =
=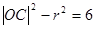
点评:在直线与圆相交时,我们通常用到弦心距、半径和弦长的一半构成的直角三角形来解题。属于基础题型。

练习册系列答案
相关题目
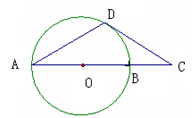
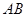 是圆O的直径,
是圆O的直径,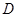 为圆O上一点,过
为圆O上一点,过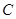 ,若DC=2,BC=1,则
,若DC=2,BC=1,则 .
.
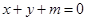 与圆
与圆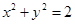 交于不同的两点A、B,O是坐标原点,且
交于不同的两点A、B,O是坐标原点,且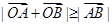 ,则实数m的取值范围是 。
,则实数m的取值范围是 。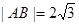 ,求a的值;
,求a的值;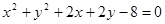 与圆C2:
与圆C2: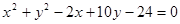 相交于A、B两点。
相交于A、B两点。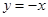 上,且过A、B两点的圆的方程;
上,且过A、B两点的圆的方程;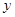 轴相切的圆的标准方程是
轴相切的圆的标准方程是
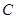 与定圆
与定圆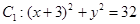 内切,与定圆
内切,与定圆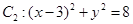 外切,A点坐标为
外切,A点坐标为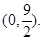 (1)求动圆
(1)求动圆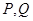 满足
满足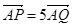 ,求
,求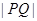 的值.
的值.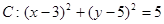 ,过圆心
,过圆心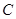 作直线
作直线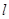 交圆于
交圆于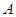 、
、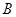 两点,与
两点,与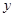 轴交于点
轴交于点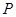 ,若
,若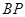 的中点,则直线
的中点,则直线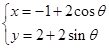 (θ为参数)的位置关系是( )
(θ为参数)的位置关系是( )