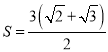Question

【题目】给出下列命题中

① 非零向量满足，则的夹角为；

②

＞0是的夹角为锐角的充要条件；

③若则必定是直角三角形；

④△ABC的外接圆的圆心为O，半径为1，若,且，则向量在向量方向上的投影为.

以上命题正确的是 __________ （注：把你认为正确的命题的序号都填上）

Answer 1

【答案】①③④

【解析】对于① 由向量满足，由向量减法的三角形法则，知向量， ， 组成一个等边三角形，向量， 夹角为，又由向量加法得平行四边形法则，以， 为邻边的平行四边形为菱形，所以的夹角为，故① 正 确；

对于②，当时，不成立；

对于③由

则

所以，即，所以是直角三角形；

对于④由题目信息可作出如右图所示,三角形AOC为等边三角形，所以∠ACB=，且BC为直径，所以∠ABC=

在直角三角形ABC中BC=2,AC=1,所以AB=，

则向量在向量方向上的投影=.

故④正确.

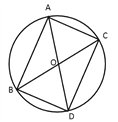
综上可知命题①③④正确.