题目内容
求过点O(0,0),A(2,0),B(0,4)的圆的方程.
思路解析:一般可考虑待定系数法,因为没有圆的特征条件,故设为一般式. 解法一:设圆的方程为x2+y2+Dx+Ey+F=0,将O(0,0)、A(2,0)、B(0,4)坐标代入得 ∴所求圆的方程为x2+y2-2x-4y=0. 解法二:显然∠AOB=90°,故所求问题即是求以AB为直径的圆的方程. 易知圆心P(1,2),半径r= 故所求的圆的方程为(x-1)2+(y-2)2=5. 深化升华 遇到过三点的圆的问题,应首先判断三点组成的三角形的形状是否为直角三角形、等腰三角形或等边三角形,从而可以迅速确定圆心的位置,以简化运算.
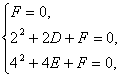 解得
解得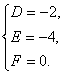
![]() |AB|=
|AB|=![]() .
. 练习册系列答案
练习册系列答案
新课堂同步学习与探究系列答案
优等生单元期末冲刺100分系列答案
绿色指标自我提升系列答案
支点系列答案
新课程资源与学案系列答案
初中复习与能力训练系列答案

初中学业水平考查全景训练系列答案
新课程学习指导系列答案
学生实验报告册辽海出版社系列答案
相关题目