题目内容
已知函数f（x）=2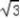 
sinxcosx+2cos2x﹣1（x∈R）
（Ⅰ）求函数f（x）的最小正周期及在区间[0，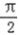
]上的最大值和最小值；
（Ⅱ）若f（x0）=
，x0∈[
，
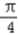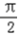]，求cos2x0的值．
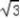sinxcosx+2cos2x﹣1（x∈R）（Ⅰ）求函数f（x）的最小正周期及在区间[0，
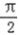]上的最大值和最小值；（Ⅱ）若f（x0）=
，x0∈[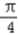 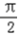， ]，求cos2x0的值．解：（Ⅰ）由f（x）=2
sinxcosx+2cos2x﹣1，
得f（x）=
（2sinxcosx）+（2cos2x）﹣1）=
sin2x+cos2x=2sin（2x+
）
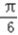所以函数f（x）的最小正周期为π．
因为f（x）=2sin（2x+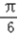
）在区间[0，
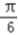]上为增函数，在区间[
，
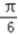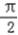]上为减函数，
又f（0）=1，f（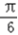
）=2，f（
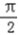）=﹣1，
所以函数f（x）在区间[0，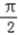
]上的最大值为2，最小值为﹣1．
（Ⅱ）由（1）可知f（x0）=2sin（2x0+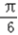
）
又因为f（x0）=
，所以sin（2x0+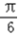
）=
由x0∈[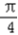
，
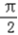]，得2x0+
∈[
，
]
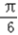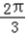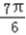从而cos（2x0+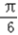
）=﹣
=﹣
．
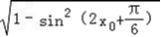所以cos2x0=cos[（2x0+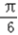
）﹣
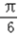]=cos（2x0+
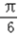）cos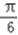
+sin（2x0+
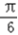）sin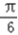
=
．
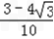sinxcosx+2cos2x﹣1，得f（x）=
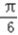（2sinxcosx）+（2cos2x）﹣1）=sin2x+cos2x=2sin（2x+）所以函数f（x）的最小正周期为π．
因为f（x）=2sin（2x+
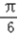）在区间[0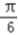，]上为增函数，在区间[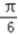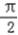，]上为减函数，又f（0）=1，f（
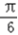）=2，f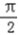（）=﹣1，所以函数f（x）在区间[0，
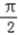]上的最大值为2，最小值为﹣1．（Ⅱ）由（1）可知f（x0）=2sin（2x0+
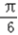）又因为f（x0）=
，所以sin（2x0+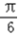）=由x0∈[
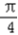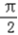，]，得2x0+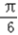∈[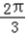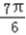，]从而cos（2x0+
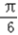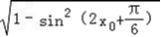）=﹣=﹣．所以cos2x0=cos[（2x0+
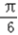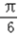）﹣]=cos（2x0+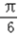）cos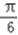+sin（2x0+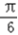）sin=．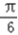
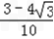练习册系列答案
相关题目