题目内容

16、如图，在三棱锥A-BCD中，DA=DC，AB=BC，求证DB⊥AC．
分析：由DE⊥AC，BE⊥AC可证AC⊥面BDE可证DB⊥AC
解答：证明；设AC的中点为E，连接DE，BE，
在△ADC中，因为DA=DC，所以DE⊥AC，
同理BE⊥AC，
∴AC⊥面BDE
∴DB⊥AC
点评：利用线面垂直，来证线线垂直，是立体几何证明中的常用方法．
练习册系列答案
相关题目
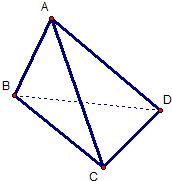精英家教网如图，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD=
3
，BD=CD=1，另一个侧面是正三角形．
（1）求证：AD⊥BC．
（2）求二面角B-AC-D的大小．
（3）在直线AC上是否存在一点E，使ED与面BCD成30°角？若存在，确定E的位置；若不存在，说明理由．
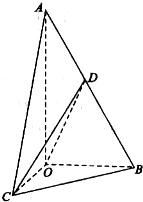精英家教网如图，在三棱锥A-BOC中，AO⊥底面BOC，∠OAB=∠OAC=30°，AB=AC=4，BC=2
2
，动点D在线段AB上．
（Ⅰ）求证：平面COD⊥平面AOB；
（Ⅱ）当点D运动到线段AB的中点时，求二面角D-CO-B的大小；
（Ⅲ）当CD与平面AOB所成角最大时，求三棱锥C-OBD的体积．
如图，在三棱锥A-BCD中，AD⊥平面ABC，∠BAC=120°，且AB=AC=AD=2，点E在BC上，且AE⊥AC．
（Ⅰ）求证：AC⊥DE；
（Ⅱ）求点B到平面ACD的距离．
如图，在三棱锥A-BOC中，AO⊥面BOC，二面角B-AO-C是直二面角，OB=OC，∠OAB=
π6
，斜边AB=4，动点D在斜边AB上．
（1）求证：平面COD⊥平面AOB；
（2）当D为AB的中点时，求：异面直线AO与CD所成角大小．
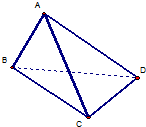如图，在三棱锥A-BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD=
3
，BD=CD=1，另一个侧面是正三角形
（1）求证：AD⊥BC
（2）求二面角B-AC-D的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网