Question

已知函数f（x）=，其中a>0.

（Ⅰ）若a=1，求曲线y=f（x）在点（2，f（2））处的切线方程；

（Ⅱ）若在区间上，f（x）>0恒成立，求a的取值范围.

Answer 1

（Ⅰ）解：当a=1时，f（x）=，f（2）=3；f’(x)=, f’(2)=6.所以曲线y=f（x）在点（2，f（2））处的切线方程为y-3=6（x-2），即y=6x-9.

（Ⅱ）解：f’(x)=.令f’(x)=0，解得x=0或x=.

以下分两种情况讨论：

（1）       若，当x变化时，f’(x)，f（x）的变化情况如下表：

X		0
f’(x)	+	0	-
f(x)		极大值

     当等价于

     解不等式组得-5<a<5.因此.

（2）       若a>2，则.当x变化时，f’(x),f（x）的变化情况如下表：

X		0
f’(x)	+	0	-	0	+
f(x)		极大值		极小值

当时，f（x）>0等价于即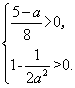

解不等式组得或.因此2<a<5.

综合（1）和（2），可知a的取值范围为0<a<5.