题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 有两个不同交点,求
有两个不同交点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的普通方程为
的普通方程为![]() ,
,![]() 的直角坐标方程为
的直角坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用平方关系消去参数![]() 即可得到曲线
即可得到曲线![]() 的普通方程,再利用极坐标与直角坐标的互化公式,即可求得曲线
的普通方程,再利用极坐标与直角坐标的互化公式,即可求得曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)解法1:根据直线的斜率公式,求得直线的斜率的取值范围,进而取得实数![]() 的取值范围.解法2:利用方程组,转化为方程
的取值范围.解法2:利用方程组,转化为方程![]() 在
在![]() 上有两个不相等实根,借助二次函数的性质,即可求解.
上有两个不相等实根,借助二次函数的性质,即可求解.
(1)解:曲线![]() 的普通方程为
的普通方程为![]() ,
,
把![]() ,
,![]() 代入
代入![]() ,得
,得
直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,即
,即![]() .
.
(2)解法1:由直线![]() :
:![]() ,知直线
,知直线![]() 恒过点
恒过点![]() .
.
由![]() ,当
,当![]() 时,得
时,得![]() ,
,
所以曲线![]() 过点
过点![]() ,
,![]() .
.
则直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的斜率为
的斜率为![]() .
.
因为直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 有两个不同交点,
有两个不同交点,
所以![]() ,即
,即![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .
.
解法2:由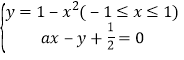 ,消去
,消去![]() 得
得![]() ,
,
依题意,得![]() 在
在![]() 上有两个不相等实根.
上有两个不相等实根.
设![]() ,
,
则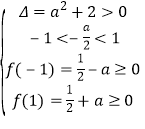 ,
,
解得![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】众所周知,城市公交车的数量太多会造成资源的浪费,太少又难以满足乘客的需求,为此,某市公交公司在某站台的50名候车乘客中随机抽取10名,统计了他们的候车时间(单位:分钟),得到下表.
候车时间 | 人数 |
| 1 |
| 4 |
| 2 |
| 2 |
| 1 |
(1)估计这10名乘客的平均候车时间(同一组中的每个数据可用该组区间的中点值代替);
(2)估计这50名乘客的候车时间少于10分钟的人数.