题目内容
已知函数f(x)= .
.
(1)求y=f(x)的最小正周期;
(2)求y=f(x)的单调递增区间;
(3)求y=f(x)的对称轴方程;
(4)x∈[ ,
, ],求方程f(x)=
],求方程f(x)= 的解集;
的解集;
(5)x∈[ ,
, ],求y=f(x)的值域;
],求y=f(x)的值域;
(6)解不等式f(x)> -
- .
.
解:(1)T= =π;
=π;
(2)令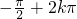 ≤
≤ ≤
≤ (k∈Z),∴
(k∈Z),∴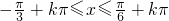
∴y=f(x)的单调递增区间为 (k∈Z);
(k∈Z);
(3)令 =
= (k∈Z),∴
(k∈Z),∴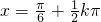 (k∈Z);
(k∈Z);
(4) =
= ,∴
,∴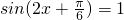 ,∴
,∴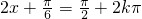
∵x∈[ ,
, ],x=
],x= ,∴方程f(x)=
,∴方程f(x)= 的解集为{
的解集为{ |;
|;
(5)x∈[ ,
, ],
], ∈[
∈[ ,
, ],∴
],∴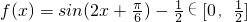 ,
,
∴y=f(x)的值域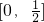 ;
;
(6)不等式f(x)> -
- ,即
,即
∴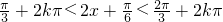 (k∈Z)
(k∈Z)
∴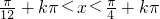 (k∈Z)
(k∈Z)
∴不等式的解集为{x|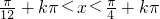 (k∈Z)}.
(k∈Z)}.
分析:(1)利用周期公式,可得结论;
(2)利用正弦函数的单调增区间,可得y=f(x)的单调递增区间;
(3)利用正弦函数的对称轴,可得y=f(x)的对称轴方程;
(4)先求出方程f(x)= 的解集,再确定x∈[
的解集,再确定x∈[ ,
, ]的解集;
]的解集;
(5)根据x∈[ ,
, ],确定
],确定 ∈[
∈[ ,
, ],即可求得函数的值域;
],即可求得函数的值域;
(6)不等式f(x)> -
- ,即
,即 ,由此可得结论.
,由此可得结论.
点评:本题考查三角函数的性质,考查解不等式,考查学生的计算能力,属于中档题.
 =π;
=π;(2)令
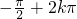 ≤
≤ ≤
≤ (k∈Z),∴
(k∈Z),∴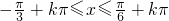
∴y=f(x)的单调递增区间为
 (k∈Z);
(k∈Z);(3)令
 =
= (k∈Z),∴
(k∈Z),∴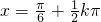 (k∈Z);
(k∈Z);(4)
 =
= ,∴
,∴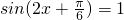 ,∴
,∴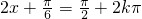
∵x∈[
 ,
, ],x=
],x= ,∴方程f(x)=
,∴方程f(x)= 的解集为{
的解集为{ |;
|;(5)x∈[
 ,
, ],
], ∈[
∈[ ,
, ],∴
],∴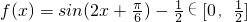 ,
,∴y=f(x)的值域
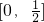 ;
;(6)不等式f(x)>
 -
- ,即
,即
∴
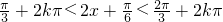 (k∈Z)
(k∈Z)∴
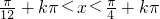 (k∈Z)
(k∈Z)∴不等式的解集为{x|
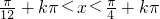 (k∈Z)}.
(k∈Z)}.分析:(1)利用周期公式,可得结论;
(2)利用正弦函数的单调增区间,可得y=f(x)的单调递增区间;
(3)利用正弦函数的对称轴,可得y=f(x)的对称轴方程;
(4)先求出方程f(x)=
 的解集,再确定x∈[
的解集,再确定x∈[ ,
, ]的解集;
]的解集;(5)根据x∈[
 ,
, ],确定
],确定 ∈[
∈[ ,
, ],即可求得函数的值域;
],即可求得函数的值域;(6)不等式f(x)>
 -
- ,即
,即 ,由此可得结论.
,由此可得结论.点评:本题考查三角函数的性质,考查解不等式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|