题目内容
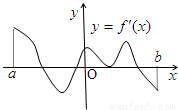
 设定义在(a,b)上的可导函数f(x)的导函数y=f'(x)的图象如右所示,则f(x)的极值点的个数为
设定义在(a,b)上的可导函数f(x)的导函数y=f'(x)的图象如右所示,则f(x)的极值点的个数为
- A.1
- B.2
- C.3
- D.4
C
分析:导数的正负与函数单调性的关系是:导数小于0则函数是减函数,导数大于0则函数是增函数,进而可以分析出正确答案.
解答:根据导数与函数单调性的关系可得函数f(x)在区间(a,b)上的单调性为:增,减,增,减,
结合函数的单调性可得函数有3个极值点.
故选C.
点评:解决此类问题的关键是准确理解导数的符号与原函数单调性之间的关系,导数小于0则函数是减函数,导数大于0则函数是增函数,进而可以分析出正确答案.
分析:导数的正负与函数单调性的关系是:导数小于0则函数是减函数,导数大于0则函数是增函数,进而可以分析出正确答案.
解答:根据导数与函数单调性的关系可得函数f(x)在区间(a,b)上的单调性为:增,减,增,减,
结合函数的单调性可得函数有3个极值点.
故选C.
点评:解决此类问题的关键是准确理解导数的符号与原函数单调性之间的关系,导数小于0则函数是减函数,导数大于0则函数是增函数,进而可以分析出正确答案.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
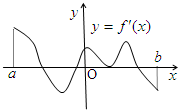 7、设定义在(a,b)上的可导函数f(x)的导函数y=f'(x)的图象如右所示,则f(x)的极值点的个数为( )
7、设定义在(a,b)上的可导函数f(x)的导函数y=f'(x)的图象如右所示,则f(x)的极值点的个数为( )