题目内容
设f(x)=ax2+bx,1≤f(-1)≤2,2≤f(1)≤4.求f(-2)的取值范围.
【答案】分析:要求f(-2)的取值范围,解题的思路为:由f(x)关系式推出f(-2)与f(1)和f(-1)的关系,再利用f(1)和f(-1)的范围,即可得f(-2)的范围.
解答:解:法一:设f(-2)=mf(-1)+nf(1)(m、n为待定系数),
则4a-2b=m(a-b)+n(a+b).
即4a-2b=(m+n)a+(n-m)b.
于是得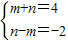 ,
,
解得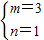 ,
,
∴f(-2)=3f(-1)+f(1).
又∵1≤f(-1)≤2,2≤f(1)≤4,
∴5≤3f(-1)+f(1)≤10,
故5≤f(-2)≤10.
点评:由a<f1(x1,y1)<b,c<f2(x1,y1)<d,求g(x1,y1)的取值范围,可利用待定系数法解决,即设g(x1,y1)=pf1(x1,y1)+qf2(x1,y1),用恒等变形求得p,q,再利用不等式的性质求得g(x1,y1)取值范围.
解答:解:法一:设f(-2)=mf(-1)+nf(1)(m、n为待定系数),
则4a-2b=m(a-b)+n(a+b).
即4a-2b=(m+n)a+(n-m)b.
于是得
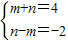 ,
,解得
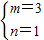 ,
,∴f(-2)=3f(-1)+f(1).
又∵1≤f(-1)≤2,2≤f(1)≤4,
∴5≤3f(-1)+f(1)≤10,
故5≤f(-2)≤10.
点评:由a<f1(x1,y1)<b,c<f2(x1,y1)<d,求g(x1,y1)的取值范围,可利用待定系数法解决,即设g(x1,y1)=pf1(x1,y1)+qf2(x1,y1),用恒等变形求得p,q,再利用不等式的性质求得g(x1,y1)取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目