题目内容
(本小题满分14分)
已知数列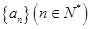 满足:
满足: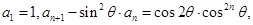 其中
其中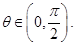
(1)当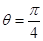 时,求
时,求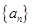 的通项公式;
的通项公式;
(2)在(1)的条件下,若数列 中,
中,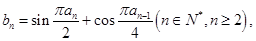 且
且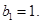 求证:对于
求证:对于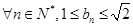 恒成立;
恒成立;
(3)对于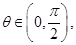 设
设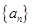 的前
的前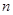 项和为
项和为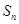 ,试比较
,试比较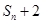 与
与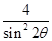 的大小.
的大小.
(1)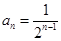 ;(2)
;(2)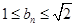 ;(3)
;(3)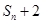 <
<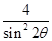 .
.
解析试题分析:(I) 当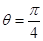 时,可求出
时,可求出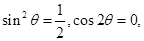 从而可得
从而可得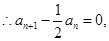 即
即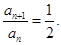 因而可确定
因而可确定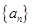 是首项为
是首项为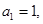 公比为
公比为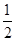 的等比数列,据此求出其通项公式;
的等比数列,据此求出其通项公式;
(II)先求出当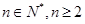 时,
时,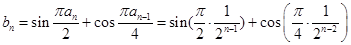 ,
,
因为b1=1也满足上式,因而当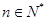 时,
时,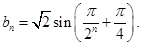
然后根据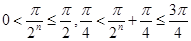 ,从得可求出
,从得可求出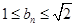 .
.
(3) 由 得:
得: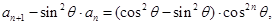
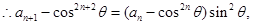
即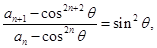
从而得到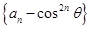 是首项为
是首项为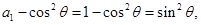 公比为
公比为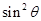 的等比数列,故
的等比数列,故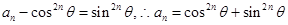 ,
,
然后可得
=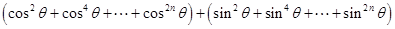 ,
,
通过分组求和即可求出Sn,到此问题基本得以解决.
(1)当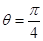 时,
时,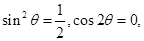
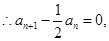 即
即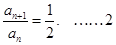 分
分
故数列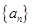 是首项为
是首项为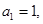 公比为
公比为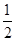 的等比数列.
的等比数列.
故数列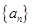 的通项公式为
的通项公式为 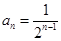 ………………………4分
………………………4分
(2)由(1)得,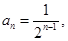
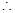 当
当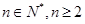 时,有
时,有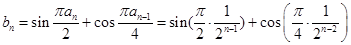
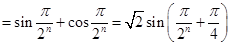 …………………6分
…………………6分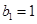 也满足上式,故当
也满足上式,故当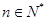 时,
时,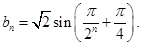
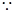
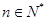 ,
,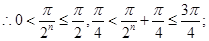
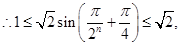 即
即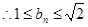 …………………………8分
…………………………8分
(3)解法一:由 得:
得: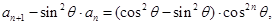
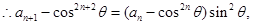
即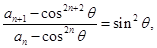
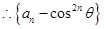 是首项为
是首项为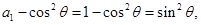 公比为
公比为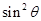 的等比数列,故
的等比数列,故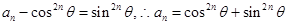 ………………9分
………………9分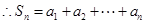
=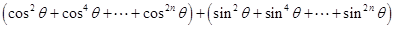
=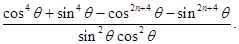 ………………………11分
………………………11分
因此,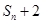 -
-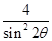 =
=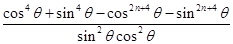
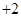 -
-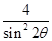
=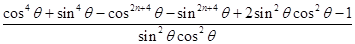
=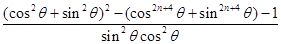
=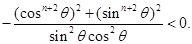
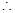
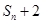 <
<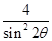 .……………………14分
.……………………14分
解法二:同解法一得 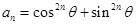 ……………………9分
……………………9分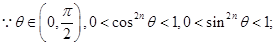 ……………………11分
……………………11分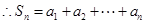
=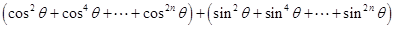
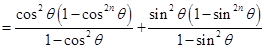
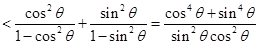

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)