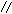题目内容
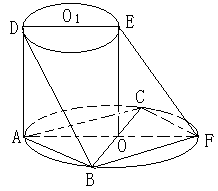
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8.BC是⊙O的直径,AB=AC=6,
OE∥AD.
(1)求二面角B-AD-F的大小;
(2)求直线BD与EF所成的角的余弦值.
(1) 二面角B—AD—F的大小为45° (2) 直线BD与EF所成的角的余弦值为![]()
解析:
(1)∵AD与两圆所在的平面均垂直,
∴AD⊥AB,AD⊥AF,
故∠BAF是二面角B—AD—F的平面角.
依题意可知,ABFC是正方形,
∴∠BAF=45°.
即二面角B—AD—F的大小为45°;
 (2)以O为原点,CB、AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),
(2)以O为原点,CB、AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),
则O(0,0,0),
A(0,-3![]() ,0),B(3
,0),B(3![]() ,0,0),D(0,-3
,0,0),D(0,-3![]() ,8),
,8),
E(0,0,8),F(0,3![]() ,0),
,0),
∴![]() =(-3
=(-3![]() ,-3
,-3![]() ,8),
,8),![]() =(0,3
=(0,3![]() ,-8).
,-8).
cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() =-
=-![]() .
.
设异面直线BD与EF所成角为![]() ,则
,则
cos![]() =|cos〈
=|cos〈![]() ,
,![]() 〉|=
〉|=![]() .
.
即直线BD与EF所成的角的余弦值为![]() .
.

练习册系列答案
相关题目
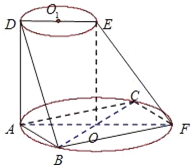 如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8.BC是⊙O的直径,AB=AC=6,OE∥AD.
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8.BC是⊙O的直径,AB=AC=6,OE∥AD. (2013•广元一模)如图所示,AF、DE分别是⊙O和⊙O1的直径,AD与两圆所在平面都垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.
(2013•广元一模)如图所示,AF、DE分别是⊙O和⊙O1的直径,AD与两圆所在平面都垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.