题目内容
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象上经过点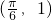 ,且最高点与最低点横坐标的绝对值为
,且最高点与最低点横坐标的绝对值为 .
.
(1)求f(x);
(2)设 ,
, ,求
,求 的值.
的值.
解:(1)因为函数的图象中最高点与最低点横坐标的绝对值为 .得到函数的周期π,
.得到函数的周期π,
所以ω=2,函数的图象经过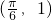 ,所以1=sin(2×
,所以1=sin(2× +φ),因为0<φ<π,所以φ=
+φ),因为0<φ<π,所以φ= ,
,
函数的解析式f(x)=sin(2x+ ).
).
(2)由 ,f(x)=sin(2x+
,f(x)=sin(2x+ ).
).
所以sin2α= ,可得(sinα+cosα)2=
,可得(sinα+cosα)2= ,
,
因为 ,所以sinα+cosα=
,所以sinα+cosα= ,
,
 =
= (sinα+cosα)=
(sinα+cosα)= ×
× =
= .
.
分析:(1)利用函数最高点与最低点横坐标之间的最短距离为 .求出函数的周期,然后求出ω,利用函数的图象经过
.求出函数的周期,然后求出ω,利用函数的图象经过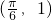 以及0<φ<π,求出φ,即可得到函数的解析式.
以及0<φ<π,求出φ,即可得到函数的解析式.
(2)通过(1)函数的解析式,利用 ,求出sinα+cosα=
,求出sinα+cosα= ,然后求出
,然后求出 的值.
的值.
点评:本题考查三角函数的解析式的求法,函数值的求法,考查分析问题解决问题的能力,计算能力.
 .得到函数的周期π,
.得到函数的周期π,所以ω=2,函数的图象经过
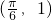 ,所以1=sin(2×
,所以1=sin(2× +φ),因为0<φ<π,所以φ=
+φ),因为0<φ<π,所以φ= ,
,函数的解析式f(x)=sin(2x+
 ).
).(2)由
 ,f(x)=sin(2x+
,f(x)=sin(2x+ ).
).所以sin2α=
 ,可得(sinα+cosα)2=
,可得(sinα+cosα)2= ,
,因为
 ,所以sinα+cosα=
,所以sinα+cosα= ,
, =
= (sinα+cosα)=
(sinα+cosα)= ×
× =
= .
.分析:(1)利用函数最高点与最低点横坐标之间的最短距离为
 .求出函数的周期,然后求出ω,利用函数的图象经过
.求出函数的周期,然后求出ω,利用函数的图象经过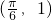 以及0<φ<π,求出φ,即可得到函数的解析式.
以及0<φ<π,求出φ,即可得到函数的解析式.(2)通过(1)函数的解析式,利用
 ,求出sinα+cosα=
,求出sinα+cosα= ,然后求出
,然后求出 的值.
的值.点评:本题考查三角函数的解析式的求法,函数值的求法,考查分析问题解决问题的能力,计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
