题目内容
若点P(cosθ,sinθ)在直线x+2y=0上,则cos2θ=( )
分析:通过点在直线上,求出tanθ,然后通过二倍角公式以及构造法利用tanθ,求出cos2θ.
解答:解:∵点P(cosθ,sinθ)在直线x+2y=0上,
∴cosθ+2sinθ=0,即tanθ=-
,
则cos2θ=
=
=
=
=
.
故选A
∴cosθ+2sinθ=0,即tanθ=-
| 1 |
| 2 |
则cos2θ=
| cos2θ |
| 1 |
| cos2θ-sin2θ |
| cos2θ+sin2θ |
| 1-tan2θ |
| 1+tan2θ |
1-
| ||
1+
|
| 3 |
| 5 |
故选A
点评:此题考查了同角三角函数间的基本关系,以及二倍角的余弦函数公式,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
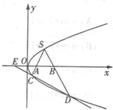 如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,弦SC,SD分别交x小轴于A,B两点,且SA=SB.
如图,S(1,1)是抛物线为y2=2px(p>0)上的一点,弦SC,SD分别交x小轴于A,B两点,且SA=SB. (2012•绍兴一模)如图,在直角三角形OAB中,P,Q是斜边AB的两个三等分点,已知
(2012•绍兴一模)如图,在直角三角形OAB中,P,Q是斜边AB的两个三等分点,已知 ,求cos∠CSD的值.
,求cos∠CSD的值.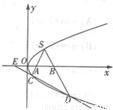
 ,求cos∠CSD的值.
,求cos∠CSD的值.