题目内容
已知数列{an}满足a1= ,且当n>1,n∈N*时,有an-1-an-4an-1an=0,
,且当n>1,n∈N*时,有an-1-an-4an-1an=0,
(1)求证:数列 {  }为等差数列;
}为等差数列;
(2)试问a1a2是否是数列 {an}中的项?如果是,是第几项;如果不是,请说明理由.
(1)证明:很显然,数列中的各项均不为0
当n≥2时,an-1-an-4 an-1 an=0,两边同除以an-1 an
得 -
- =4,即
=4,即 -
- =4
=4
对n>1,n∈N*成立,
∴{ }是以
}是以 =5为首项,4为公差的等差数列.
=5为首项,4为公差的等差数列.
(2)解:由(1)得 =
= +(n-1)d=4n+1,
+(n-1)d=4n+1,
∴an=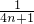 ,
,
∴a1a2= ×
× =
=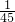 .
.
设a1a2是数列{an}的第t项,
则 =
=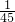 ,
,
解得t=11∈N*.
∴a1a2是数列{an}的第11项.
分析:(1)当n≥2时an-1-an-4 an-1 an=0,两边同除以an-1 an,可得 -
- =4,即
=4,即 -
- =4,从而可证{
=4,从而可证{ }是以
}是以 =5为首项,4为公差的等差数列.
=5为首项,4为公差的等差数列.
(2)由(1)可求数列的通项公式an=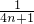 ,从而a1a2=
,从而a1a2= ×
× =
=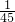 ,进而可判断a1a2是数列{an}的第11项.
,进而可判断a1a2是数列{an}的第11项.
点评:本题考查的重点是等差数列的判断,考查等差数列的通项,解题的关键是将数列递推式变形.
当n≥2时,an-1-an-4 an-1 an=0,两边同除以an-1 an
得
 -
- =4,即
=4,即 -
- =4
=4对n>1,n∈N*成立,
∴{
 }是以
}是以 =5为首项,4为公差的等差数列.
=5为首项,4为公差的等差数列.(2)解:由(1)得
 =
= +(n-1)d=4n+1,
+(n-1)d=4n+1,∴an=
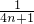 ,
,∴a1a2=
 ×
× =
=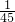 .
.设a1a2是数列{an}的第t项,
则
 =
=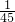 ,
,解得t=11∈N*.
∴a1a2是数列{an}的第11项.
分析:(1)当n≥2时an-1-an-4 an-1 an=0,两边同除以an-1 an,可得
 -
- =4,即
=4,即 -
- =4,从而可证{
=4,从而可证{ }是以
}是以 =5为首项,4为公差的等差数列.
=5为首项,4为公差的等差数列.(2)由(1)可求数列的通项公式an=
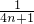 ,从而a1a2=
,从而a1a2= ×
× =
=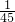 ,进而可判断a1a2是数列{an}的第11项.
,进而可判断a1a2是数列{an}的第11项.点评:本题考查的重点是等差数列的判断,考查等差数列的通项,解题的关键是将数列递推式变形.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目