题目内容
椭圆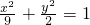 的焦点为F1,F2,点P在椭圆上,若|PF1|=4,则△PF1F2的面积等于________.
的焦点为F1,F2,点P在椭圆上,若|PF1|=4,则△PF1F2的面积等于________.
2
分析:根据椭圆方程,可得△PF1F2的三边长,利用余弦定理可得, ,进而利用三角形的面积公式可得结论
,进而利用三角形的面积公式可得结论
解答:由题意,|PF1|=4,|PF2|=6-4=2,|F1F2|=2
利用余弦定理可得,
∴
∴△PF1F2的面积等于
故答案为:
点评:本题以椭圆的标准方程为载体,考查焦点三角形的面积问题,解题的关键是得出焦点三角形的三边长,进而利用面积公式求解.

分析:根据椭圆方程,可得△PF1F2的三边长,利用余弦定理可得,
 ,进而利用三角形的面积公式可得结论
,进而利用三角形的面积公式可得结论解答:由题意,|PF1|=4,|PF2|=6-4=2,|F1F2|=2

利用余弦定理可得,

∴

∴△PF1F2的面积等于

故答案为:

点评:本题以椭圆的标准方程为载体,考查焦点三角形的面积问题,解题的关键是得出焦点三角形的三边长,进而利用面积公式求解.

练习册系列答案
相关题目
