题目内容
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求四面体BCEF的体积.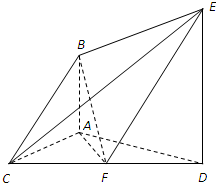
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求四面体BCEF的体积.

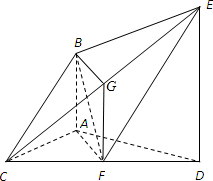
(1)证明:取EC中点G,连BG,GF.
∵F是CD的中点,∴FG∥DE,且FG=
| 1 |
| 2 |
又∵AB∥DE,且AB=
| 1 |
| 2 |
∴四边形ABGF为平行四边形.…(3分)
∴AF∥BG.
又BG?平面BCE,AF?平面BCE.
∴AF∥平面BCE. …(5分)
(2)证明:∵AB⊥平面ACD,AF?平面ACD,
∴AB⊥AF.
∵AB∥DE,∴AF⊥DE. …(6分)
又∵△ACD为正三角形,∴AF⊥CD. …(7分)
∵BG∥AF,∴BG⊥DE,BG⊥CD. …(8分)
∵CD∩DE=D,∴BG⊥平面CDE. …(9分)
∵BG?平面BCE,∴平面BCE⊥平面CDE; …(11分)
(3)四面体BCEF的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.