题目内容
（本小题12分）
在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且
(1)求角C的大小；
（2）若c＝
,且△ABC的面积为
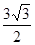
,求a＋b的值。
【答案】
（1）
；（2）5.
【解析】
试题分析：（1）把已知的等式变形为： 
，并利用正弦定理化简，根据sinA不为0，可得出sinC的值，由三角形为锐角三角形，得出C为锐角，利用特殊角的三角函数值即可求出C的度数；
（2）由面积公式求得ab=6，再由余弦定理
求得a+b的值．.
（1）依题意得
…………3分
………………5分
（2）
……………7分
考点：正余弦定理在解三角形中的应用，面积公式。
点评：解决好本小题的关键是掌握好余弦定理的变形形式,如：
.
练习册系列答案
相关题目
中，
的对边分别为
，已知
。
的值：
中，直线
与抛物线
相交于
．
两点。
，那么
”是真命题。
ABC中，设
，求A的值。