题目内容
已知函数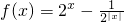 .
.
(1)设集合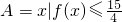 ,B={x|x2-6x+p<0},若A∩B≠∅,求实数p的取值范围;
,B={x|x2-6x+p<0},若A∩B≠∅,求实数p的取值范围;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
解:(1)当x≥0时,f(x)≤ ,即
,即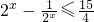 ,解得0≤x≤2;
,解得0≤x≤2;
当x<0时,f(x)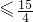 即0
即0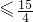 成立,
成立,
综上,f(x)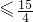 的解集为{x|x≤2},即A=(-∞,2].
的解集为{x|x≤2},即A=(-∞,2].
设g(x)=x2-6x+p,
因为A∩B≠∅,所以g(2)<0,即4-6×2+p<0,解得p<8,
所以实数p的取值范围为:(-∞,8).
(2)因为t∈[1,2],所以f(t)=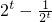 ,
,
2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,即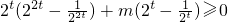 恒成立,
恒成立,
即(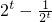 )(22t+1+m)≥0,
)(22t+1+m)≥0,
因为22t-1≥3,所以22t+1+m≥0恒成立,即m≥-(1+22t),
因为t∈[1,2],所以-(1+22t)∈[-17,-5],则m≥-5.
故实数m的取值范围为[-5,+∞).
分析:(1)解不等式f(x)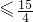 得到A,令g(x)=x2-6x+p,由A∩B≠∅,得g(2)<0,解出即可;
得到A,令g(x)=x2-6x+p,由A∩B≠∅,得g(2)<0,解出即可;
(2)对不等式进行等价转化,分离出参数m后,转化为函数最值问题解决;
点评:本题考查函数恒成立问题及不等式的求解、集合运算,具有一定综合性,恒成立问题的常用解决方法是转化为函数最值处理.
 ,即
,即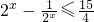 ,解得0≤x≤2;
,解得0≤x≤2;当x<0时,f(x)
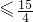 即0
即0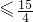 成立,
成立,综上,f(x)
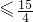 的解集为{x|x≤2},即A=(-∞,2].
的解集为{x|x≤2},即A=(-∞,2].设g(x)=x2-6x+p,
因为A∩B≠∅,所以g(2)<0,即4-6×2+p<0,解得p<8,
所以实数p的取值范围为:(-∞,8).
(2)因为t∈[1,2],所以f(t)=
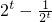 ,
,2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,即
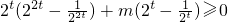 恒成立,
恒成立,即(
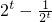 )(22t+1+m)≥0,
)(22t+1+m)≥0,因为22t-1≥3,所以22t+1+m≥0恒成立,即m≥-(1+22t),
因为t∈[1,2],所以-(1+22t)∈[-17,-5],则m≥-5.
故实数m的取值范围为[-5,+∞).
分析:(1)解不等式f(x)
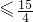 得到A,令g(x)=x2-6x+p,由A∩B≠∅,得g(2)<0,解出即可;
得到A,令g(x)=x2-6x+p,由A∩B≠∅,得g(2)<0,解出即可;(2)对不等式进行等价转化,分离出参数m后,转化为函数最值问题解决;
点评:本题考查函数恒成立问题及不等式的求解、集合运算,具有一定综合性,恒成立问题的常用解决方法是转化为函数最值处理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目