题目内容
设f(x)是定义在区间(1,+∞)上的函数,其导函数为f′(x),如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得f′(x)=h(x)(x2-ax+1),则称函数f(x)具有性质P(a),
(Ⅰ)设函数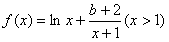 ,其中b为实数,
,其中b为实数,
(ⅰ)求证:函数f(x)具有性质P(b);
(ⅱ)求函数f(x)的单调区间;
(Ⅱ)已知函数g(x)具有性质P(2)。给定x1,x2∈(1,+∞),x1<x2,设m为实数,α=mx1+(1-m)x2,β=(1-m)x1+mx2,且α>1,β>1,若|g(α) -g(β)|<|g(x1)-g(x2)|,求m的取值范围。
(Ⅰ)设函数
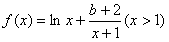 ,其中b为实数,
,其中b为实数,(ⅰ)求证:函数f(x)具有性质P(b);
(ⅱ)求函数f(x)的单调区间;
(Ⅱ)已知函数g(x)具有性质P(2)。给定x1,x2∈(1,+∞),x1<x2,设m为实数,α=mx1+(1-m)x2,β=(1-m)x1+mx2,且α>1,β>1,若|g(α) -g(β)|<|g(x1)-g(x2)|,求m的取值范围。
解:(Ⅰ)(ⅰ)由 ,得
,得 ,
,
因为x>1时, ,
,
所以函数f(x)具有性质P(b).
(ⅱ)当b≤2时,由x>1得x2-bx+1≥x2-2x+1=(x-1)2>0,
所以f′(x)>0,从而函数f(x)在区间(1,+∞)上单调递增;
当b>2时,解方程x2-bx+1=0得 ,
,
因为 ,
, ,
,
所以当x∈(1,x2)时,f′(x)<0;当x∈(x2,+∞)时,f′(x)>0;当x=x2时,f′(x)=0,
从而函数f(x)在区间(1,x2)上单调递减,在区间(x2,+∞)上单调递增;
综上所述,当b≤2时,函数f(x)的单调增区间为(1,+∞);
当b>2时,函数f(x)的单调减区间为 ,单调增区间为
,单调增区间为 。
。
(Ⅱ)由题设知,g(x)的导函数g′(x)=h(x)(x2-2x+1),其中函数h(x)>0对于任意的x∈(1,+∞)都成立,
所以,当x>1时,g′(x)=h(x)(x-1)2>0,
从而g(x)在区间(1,+∞) 上单调递增.
①当m∈(0,1)时,有α=mx1+(1-m)x2> mx1+(1-m)x1=x1,
α<mx2+(1-m)x2=x2,得α∈(x1,x2),同理可得β∈(x1,x2),
所以由g(x)的单调性知g(α),g(β)∈(g(x1),g(x2)),
从而有|g(α)-g(β)|<|g(x1)-g(x2)|,符合题设;
②当m≤0时,α=mx1+(1-m)x2≥mx2+(1-m)x2=x2,β=(1-m)x1+mx2≤(1-m)x1+mx1=x1,
于是由α>1,β>1及g(x)的单调性知g(β)≤g(x1)<g(x2)≤g(α),
所以|g(α)-g(β)|≥|g(x1)-g(x2)|,与题设不符;
③当m≥1时,同理可得α≤x1,β≥x2,进而得|g(α)-g(β)|≥|g(x1)-g(x2)|,与题设不符;
因此,综合①②③得所求的m的取值范围为(0,1)。
 ,得
,得 ,
,因为x>1时,
 ,
,所以函数f(x)具有性质P(b).
(ⅱ)当b≤2时,由x>1得x2-bx+1≥x2-2x+1=(x-1)2>0,
所以f′(x)>0,从而函数f(x)在区间(1,+∞)上单调递增;
当b>2时,解方程x2-bx+1=0得
 ,
,因为
 ,
, ,
,所以当x∈(1,x2)时,f′(x)<0;当x∈(x2,+∞)时,f′(x)>0;当x=x2时,f′(x)=0,
从而函数f(x)在区间(1,x2)上单调递减,在区间(x2,+∞)上单调递增;
综上所述,当b≤2时,函数f(x)的单调增区间为(1,+∞);
当b>2时,函数f(x)的单调减区间为
 ,单调增区间为
,单调增区间为 。
。(Ⅱ)由题设知,g(x)的导函数g′(x)=h(x)(x2-2x+1),其中函数h(x)>0对于任意的x∈(1,+∞)都成立,
所以,当x>1时,g′(x)=h(x)(x-1)2>0,
从而g(x)在区间(1,+∞) 上单调递增.
①当m∈(0,1)时,有α=mx1+(1-m)x2> mx1+(1-m)x1=x1,
α<mx2+(1-m)x2=x2,得α∈(x1,x2),同理可得β∈(x1,x2),
所以由g(x)的单调性知g(α),g(β)∈(g(x1),g(x2)),
从而有|g(α)-g(β)|<|g(x1)-g(x2)|,符合题设;
②当m≤0时,α=mx1+(1-m)x2≥mx2+(1-m)x2=x2,β=(1-m)x1+mx2≤(1-m)x1+mx1=x1,
于是由α>1,β>1及g(x)的单调性知g(β)≤g(x1)<g(x2)≤g(α),
所以|g(α)-g(β)|≥|g(x1)-g(x2)|,与题设不符;
③当m≥1时,同理可得α≤x1,β≥x2,进而得|g(α)-g(β)|≥|g(x1)-g(x2)|,与题设不符;
因此,综合①②③得所求的m的取值范围为(0,1)。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(
天津六区联考模拟)设f(x)是定义在R上的单调递减的奇函数,若 ,
, ,
, ,则
,则
[
]|
A . |
B . |
|
C . |
D . |