题目内容
物体沿直线运动过程中,位移s与时间t的关系式是s(t)=3t2+t.我们计算在t时刻的附近区间[t,t+△t]内的平均速度 =________,当△t趋近于0时,平均速度
=________,当△t趋近于0时,平均速度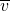 趋近于确定的值,即瞬时速度,由此可得到t时刻的瞬时速度为________.
趋近于确定的值,即瞬时速度,由此可得到t时刻的瞬时速度为________.
6t+1+3△t, 6t+1
分析:由题意知,先计算出平均速度 的化简式,再由导数的物理意义求出导数即可得到瞬时速度
的化简式,再由导数的物理意义求出导数即可得到瞬时速度
解答:∵体沿直线运动过程中,位移s与时间t的关系式是s(t)=3t2+t.
∴在t时刻的附近区间[t,t+△t]内的平均速度
又s'(t)=6t+1
故答案为6t+1+3△t; 6t+1
点评:本题考查变化的快慢与变化率,解题的关键是理解平均速度与瞬时速度的意义,且能理解导数的物理意义.求函数的导数,记忆常用函数的求导公式对顺利解题很关键.
分析:由题意知,先计算出平均速度
 的化简式,再由导数的物理意义求出导数即可得到瞬时速度
的化简式,再由导数的物理意义求出导数即可得到瞬时速度解答:∵体沿直线运动过程中,位移s与时间t的关系式是s(t)=3t2+t.
∴在t时刻的附近区间[t,t+△t]内的平均速度

又s'(t)=6t+1
故答案为6t+1+3△t; 6t+1
点评:本题考查变化的快慢与变化率,解题的关键是理解平均速度与瞬时速度的意义,且能理解导数的物理意义.求函数的导数,记忆常用函数的求导公式对顺利解题很关键.

练习册系列答案
相关题目
 . 我们计算在
. 我们计算在 的附近区间
的附近区间 内的平均速度
内的平均速度 ,当
,当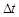 趋近于0时,平均速度
趋近于0时,平均速度 趋近于确定的值,即瞬时速度,由此可得到
趋近于确定的值,即瞬时速度,由此可得到 . 我们计算在
. 我们计算在 的附近区间
的附近区间 内的平均速度
内的平均速度 ,当
,当 趋近于0时,平均速度
趋近于0时,平均速度 趋近于确定的值,即瞬时速度,由此可得到
趋近于确定的值,即瞬时速度,由此可得到 . 我们计算在
. 我们计算在 的附近区间
的附近区间 内的平均速度
内的平均速度 ,当
,当 趋近于0时,平均速度
趋近于0时,平均速度 趋近于确定的值,即瞬时速度,由此可得到
趋近于确定的值,即瞬时速度,由此可得到