题目内容
已知函数f(x)的图象在[a,b]上连续不断,定义:f1(x)=min{f(t)|a≤t≤x}(x∈[a,b]),f2(x)=max{f(t)|a≤t≤x}(x∈[a,b]),其中,min{f(x)|x∈D}表示函数f(x)在D上的最小值,max{f(x)|x∈D}表示函数f(x)在D上的最大值.若存在最小正整数k,使得f2(x)﹣f1(x)≤k(x﹣a)对任意的x∈[a,b]成立,则称函数f(x)为[a,b]上的“k阶收缩函数”.
(1)若f(x)=cosx,x∈[0,π],试写出f1(x),f2(x)的表达式;
(2)已知函数f(x)=x2,x∈[﹣1,4],试判断f(x)是否为[﹣1,4]上的“k阶收缩函数”,如果是,求出对应的k;如果不是,请说明理由;
(3)已知b>0,函数f(x)=﹣x3+3x2是[0,b]上的2阶收缩函数,求b的取值范围.
(1)若f(x)=cosx,x∈[0,π],试写出f1(x),f2(x)的表达式;
(2)已知函数f(x)=x2,x∈[﹣1,4],试判断f(x)是否为[﹣1,4]上的“k阶收缩函数”,如果是,求出对应的k;如果不是,请说明理由;
(3)已知b>0,函数f(x)=﹣x3+3x2是[0,b]上的2阶收缩函数,求b的取值范围.
解:(Ⅰ)由题意可得:f1(x)=cosx,x∈[0,π],f2(x)=1,x∈[0,π].
(Ⅱ)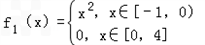 ,
,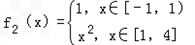
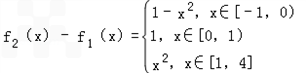
当x∈[﹣1,0]时,1﹣x2≤k(x+1),∴k≥1﹣x,k≥2;
当x∈(0,1)时,1≤k(x+1),∴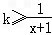 ,∴k≥1;
,∴k≥1;
当x∈[1,4]时,x2≤k(x+1),∴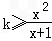 ,∴
,∴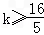 .
.
综上所述,∴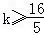
即存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数.
(Ⅲ)f'(x)=﹣3x2+6x=﹣3x(x﹣2),令f'(x)=0得x=0或x=2.

函数f(x)的变化情况如下:
令f(x)=0,解得x=0或3.
(ⅰ)b≤2时,f(x)在[0,b]上单调递增,
因此,f2(x)=f(x)=﹣x3+3x2,f1(x)=f(0)=0.
因为f(x)=﹣x3+3x2是[0,b]上的2阶收缩函数,
所以,①f2(x)﹣f1(x)≤2(x﹣0)对x∈[0,b]恒成立;
②存在x∈[0,b],使得f2(x)﹣f1(x)>(x﹣0)成立.
①即:﹣x3+3x2≤2x对x∈[0,b]恒成立,
由﹣x3+3x2≤2x,解得:0≤x≤1或x≥2,
要使﹣x3+3x2≤2x对x∈[0,b]恒成立,需且只需0<b≤1.
②即:存在x∈[0,b],使得x(x2﹣3x+1)<0成立.
由x(x2﹣3x+1)<0得:x<0或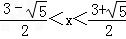 ,
,
所以,需且只需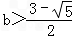 .
.
综合①②可得: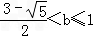 .
.
(ⅱ)当b>2时,显然有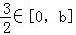 ,由于f(x)在[0,2]上单调递增,
,由于f(x)在[0,2]上单调递增,
根据定义可得: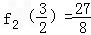 ,
,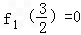 ,
,
可得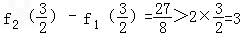 ,
,
此时,f2(x)﹣f1(x)≤2(x﹣0)不成立.
综合ⅰ)ⅱ)可得: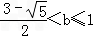 .
.
注:在ⅱ)中只要取区间(1,2)内的一个数来构造反例均可,这里用只是因为简单而已.
(Ⅱ)
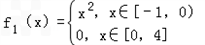 ,
,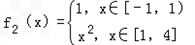
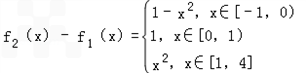
当x∈[﹣1,0]时,1﹣x2≤k(x+1),∴k≥1﹣x,k≥2;
当x∈(0,1)时,1≤k(x+1),∴
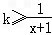 ,∴k≥1;
,∴k≥1;当x∈[1,4]时,x2≤k(x+1),∴
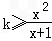 ,∴
,∴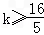 .
.综上所述,∴
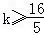
即存在k=4,使得f(x)是[﹣1,4]上的4阶收缩函数.
(Ⅲ)f'(x)=﹣3x2+6x=﹣3x(x﹣2),令f'(x)=0得x=0或x=2.

函数f(x)的变化情况如下:
令f(x)=0,解得x=0或3.
(ⅰ)b≤2时,f(x)在[0,b]上单调递增,
因此,f2(x)=f(x)=﹣x3+3x2,f1(x)=f(0)=0.
因为f(x)=﹣x3+3x2是[0,b]上的2阶收缩函数,
所以,①f2(x)﹣f1(x)≤2(x﹣0)对x∈[0,b]恒成立;
②存在x∈[0,b],使得f2(x)﹣f1(x)>(x﹣0)成立.
①即:﹣x3+3x2≤2x对x∈[0,b]恒成立,
由﹣x3+3x2≤2x,解得:0≤x≤1或x≥2,
要使﹣x3+3x2≤2x对x∈[0,b]恒成立,需且只需0<b≤1.
②即:存在x∈[0,b],使得x(x2﹣3x+1)<0成立.
由x(x2﹣3x+1)<0得:x<0或
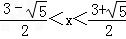 ,
,所以,需且只需
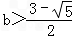 .
.综合①②可得:
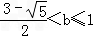 .
. (ⅱ)当b>2时,显然有
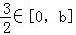 ,由于f(x)在[0,2]上单调递增,
,由于f(x)在[0,2]上单调递增,根据定义可得:
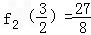 ,
,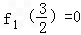 ,
,可得
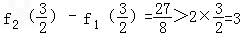 ,
,此时,f2(x)﹣f1(x)≤2(x﹣0)不成立.
综合ⅰ)ⅱ)可得:
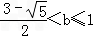 .
.注:在ⅱ)中只要取区间(1,2)内的一个数来构造反例均可,这里用只是因为简单而已.

练习册系列答案
相关题目
已知函数f(x)的图象关于直线x=2对称,且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4,则下列表示大小关系的式子正确的是( )
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(