题目内容
 如图,已知正四棱柱ABCD-A1B1C1D1的底面边长是2,体积是16,M,N分别是棱BB1、B1C1的中点.
如图,已知正四棱柱ABCD-A1B1C1D1的底面边长是2,体积是16,M,N分别是棱BB1、B1C1的中点.
(1)求异面直线MN与A1C1所成角的大小(结果用反三角表示);
(2)求过A1,B,C1的平面与该正四棱柱所截得的多面体A1C1D1-ABCD的体积.
解:(1)由题意得16=22×B1B,∴B1B=4.
在Rt△ABC中,由勾股定理可得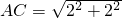 =
= =A1C1.
=A1C1.
同理可得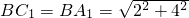 =
= .
.
连接BC1,∵M,N分别是棱BB1、B1C1的中点,∴BC1∥MN,
∴∠A1C1B或其补角是异面直线MN与A1C1所成的角.
连接BA1,在△A1BC1中,由余弦定理得cos∠A1C1B=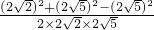 =
= .
.
∴异面直线MN与A1C1所成的角为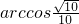 .
.
(2)∵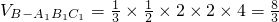 ;
;
∴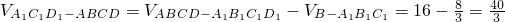 ,
,
∴多面体A1C1D1-ABCD的体积为 .
.
分析:(1)利用三角形的中位线定理、勾股定理、异面直线所成的角的定义即可得出;
(2)先计算出三棱锥B-A1B1C1体积,即可得出要求的体积.
点评:熟练掌握三角形的中位线定理、勾股定理、异面直线所成的角的定义及三棱锥的体积是解题的关键.
在Rt△ABC中,由勾股定理可得
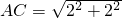 =
= =A1C1.
=A1C1.同理可得
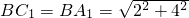 =
= .
.连接BC1,∵M,N分别是棱BB1、B1C1的中点,∴BC1∥MN,
∴∠A1C1B或其补角是异面直线MN与A1C1所成的角.
连接BA1,在△A1BC1中,由余弦定理得cos∠A1C1B=
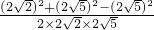 =
= .
.∴异面直线MN与A1C1所成的角为
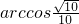 .
.(2)∵
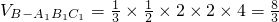 ;
;∴
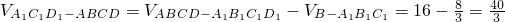 ,
,∴多面体A1C1D1-ABCD的体积为
 .
.分析:(1)利用三角形的中位线定理、勾股定理、异面直线所成的角的定义即可得出;
(2)先计算出三棱锥B-A1B1C1体积,即可得出要求的体积.
点评:熟练掌握三角形的中位线定理、勾股定理、异面直线所成的角的定义及三棱锥的体积是解题的关键.

练习册系列答案
相关题目
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a. 如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.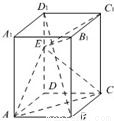 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.