题目内容
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
【答案】(1)a=2,b=1.(2)![]()
【解析】试题分析:(1)由函数是奇函数可得![]() ,将
,将![]() 代入两个特殊值得到关于
代入两个特殊值得到关于![]() 的方程组求解其值;(2)首先利用定义法判断函数的单调性,利用奇函数将不等式变形为f(x2-x)< f(-2x2+t),,利用单调性得到关于
的方程组求解其值;(2)首先利用定义法判断函数的单调性,利用奇函数将不等式变形为f(x2-x)< f(-2x2+t),,利用单调性得到关于![]() 的恒成立不等式,分离参数
的恒成立不等式,分离参数![]() 后通过求函数最值得到
后通过求函数最值得到![]() 的取值范围
的取值范围
试题解析:(1)∵f(x)是奇函数且0∈R,∴f(0)=0即![]()
∴![]()
又由f(1)=-f(-1)知
![]() a=2
a=2
∴f(x)=![]()
(2)证明设x1,x2∈(-∞,+∞)且x1<x2
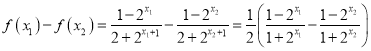
![]() ·
·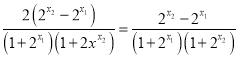
∵y=2x在(-∞,+∞)上为增函数且x1<x2,∴![]()
且y=2x>0恒成立,∴![]()
∴f(x1)-f(x2)>0 即f(x1)>f(x2)
∴f(x)在(-∞,+∞)上为减函数
∵f(x)是奇函数f(x2-x)+f(2x2-t)<0等价于f(x2-x)<-f(2x2-t)=f(-2x2+t)
又∵f(x)是减函数,∴x2-x>-2x2+t
即一切x∈R,3x2-x-t>0恒成立
∴△=1+12t<0,即t<![]()

 习题精选系列答案
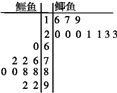
习题精选系列答案【题目】为了选拔参加自行车比赛的选手,对自行车运动员甲、乙两人在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图,由茎叶图你能获得哪些信息;
(2)估计甲、乙两运动员的最大速度的平均数和方差,并判断谁参加比赛更合适.
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?