题目内容
设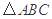 的内角
的内角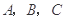 所对的边长分别为
所对的边长分别为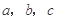 ,且
,且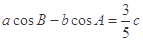 .
.
(1)求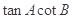 的值;
的值;
(2)求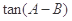 的最大值.
的最大值.
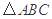 的内角
的内角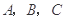 所对的边长分别为
所对的边长分别为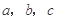 ,且
,且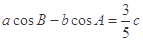 .
.(1)求
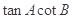 的值;
的值;(2)求
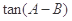 的最大值.
的最大值.(1) ;(2)
;(2)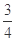 .
.
 ;(2)
;(2)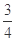 .
.试题分析:(1)利用正弦定理及三角形内角和关系,将原式化成
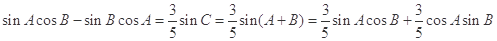 ,化简得
,化简得 ,从而
,从而 ;(2)利用两角差的正切展开
;(2)利用两角差的正切展开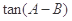 ,将
,将 代入,接着利用均值不等式即可算出最大值.
代入,接着利用均值不等式即可算出最大值.试题解析:(1)在
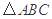 中,由正弦定理及
中,由正弦定理及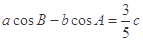 可得
可得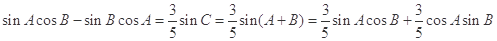
即
 ,则
,则 ;
;(2)由
 得
得

当且仅当
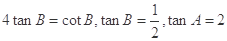 时,等号成立,
时,等号成立,故当
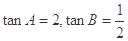 时,
时,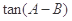 的最大值为
的最大值为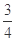 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =
= ,
, π<x<
π<x< π,求
π,求 的值.
的值.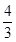 ,sin(α+β)=
,sin(α+β)=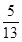 ,其中α,β∈(0,π),则sin α的值为________.
,其中α,β∈(0,π),则sin α的值为________. 是方程
是方程 的两根,则
的两根,则 =_______.
=_______.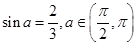 ,则
,则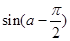 =____________.
=____________.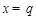 时,函数
时,函数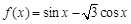 取得最大值,则
取得最大值,则 .
. 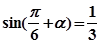 ,则
,则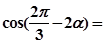 ___________.
___________. ,
, 且
且 ,
, ,则
,则 的值为 .
的值为 . ,则
,则 ( )
( )


