题目内容
如图,在四棱锥![]() 中,
中,![]()
![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形,![]() .
.
(Ⅰ)求证:![]() 平面
平面![]()
(Ⅱ)若![]() 求
求![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当平面![]() 与平面
与平面![]() 垂直时,求
垂直时,求![]() 的长.
的长.
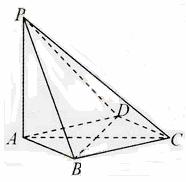
证明:(Ⅰ)因为四边形ABCD是菱形,
所以AC⊥BD.
又因为PA⊥平面ABCD.
所以PA⊥BD.
所以BD⊥平面PAC.
(Ⅱ)设AC∩BD=O.
因为∠BAD=60°,PA=PB=2,
所以BO=1,AO=CO=![]() .
.
如图,以O为坐标原点,建立空间直角坐标系O—xyz,则
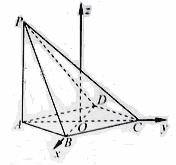 |
P(0,—![]() ,2),A(0,—
,2),A(0,—![]() ,0),B(1,0,0),C(0,
,0),B(1,0,0),C(0,![]() ,0).
,0).
所以![]()
设PB与AC所成角为![]() ,则
,则
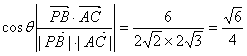 .
.
(Ⅲ)由(Ⅱ)知![]()
设P(0,-![]() ,t)(t>0),
,t)(t>0),
则![]()
设平面PBC的法向量![]() ,
,
则![]()
所以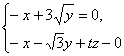
令![]() 则
则![]()
所以![]()
同理,平面PDC的法向量![]()
因为平面PCB⊥平面PDC,
所以![]() =0,即
=0,即![]()
解得![]()
所以PA=![]()

练习册系列答案
相关题目
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.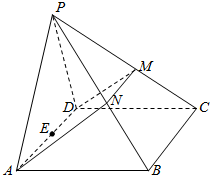 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点. 如图,在四棱锥
如图,在四棱锥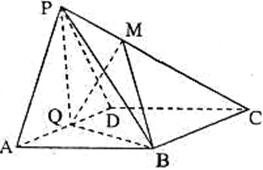 试确定
试确定