Question

设Ｐ，Ｑ为圆周上的两动点，且满足与圆内一定点，使，求过Ｐ和Ｑ的两条切线的交点M的轨迹。

Answer 1

轨迹是以为圆心，为半径的圆周

解析:

解法一：连接PQ，OM，由圆的切线性质知 ，且PQ与OM交点E为PQ的中点。

…………5分

设，则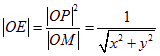，。从而得到E点的坐标为

。                                  …………10分

由于，所以。又，于是有

，即有

                    ………… 15分

化简得。

上述为以为圆心，为半径的圆周。           …………20分

解法二： 设Ｐ，Ｑ的坐标为。由题意知，过Ｐ，Ｑ的切线方程分别为

　　　………… ①，     ………… ②

       ………… ③

       ………… ④       ………… 5分

由，得

  ………… ⑤

若①和②的交点仍记为，由此得到 ()               ………… 10分

代入③和④，得

       

   

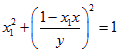
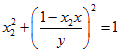
联立上述两式，即得

            ………… 15分

因为，所以，即。

同理可得 。于是有

再由⑤式，推出。

由上可得，。

即有。

上述为以为圆心，为半径的圆周。                     …………20分

当时，也符合题设所求的轨迹。