题目内容
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.如果希望大部分居民的日常生活不受影响,那么标准a定为多少比较合适呢?你认为,为了较合理地确定这个标准,需要做哪些工作?
解析:为了制定出居民用水量的标准,需要了解广大居民的实际月用水量大部分在什么数值范围内.但由于居民户较多,全部调查不易操作,故可采取抽样调查的方式获取一个有代表性的样本,然后通过样本的情况估计所有居民的月用水量,以便制定出这个标准.
很显然,如果标准太高,会影响居民的日常生活;如果标准太低,则不利于节水.为了确定一个较合理的标准,必须先了解居民日常用水的分布情况,比如月平均用水量在哪个范围内的居民最多,他们占全市居民的百分比情况等.
由于城市居户较多,通常采用抽样调查的方式,通过分析样本数据来估计全市居民用水量的分布情况.假设通过抽样我们获得了100位居民今年的月均用水量(单位:t):
100位居民2006年的月均用水量(单位:t):
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
面对这些随意记录的数据,除了发现月用水量的最大值是4.3和最小值是0.2之外,很难再看出其他信息.为此我们需要对这些数据进行分析整理.分析数据的一种最基本的方法是用图(即频率分布直方图)将它们画出来,以便从数据中提取信息和传递信息,或者是用紧凑的表格(即频率分布表)改变数据的排列方式.下图是100位居民2006年的月均用水量的频率分布表:
分组 | 频数 | 频率 |
[0,0.5) | 4 | 0.04 |
[0.5,1) | 8 | 0.08 |
[1,1.5) | 15 | 0.15 |
[1.5,2) | 22 | 0.22 |
[2,2.5) | 25 | 0.25 |
[2.5,3) | 14 | 0.14 |
[3,3.5) | 6 | 0.06 |
[3.5,4) | 4 | 0.04 |
[4,4.5) | 2 | 0.02 |
合计 | 100 | 1.00 |
频率分布直方图如下:
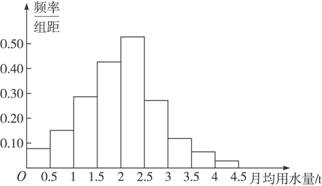
上面的图和表显示了样本数据落在各个小组的比例大小.从中我们可以看到,月用水量在区间[2, 2.5]内的居民最多,在[1.5, 2]的次之,大部分居民的月用水量都在[1, 3]之间,其中月用水量在3 t以上的居民所占的比例为6%+4%+2%=12%,即大约占12%的居民月用水量在3 t以上,88%的居民月用水量在3 t以下.因此居民月用水量标准定为3 t是一个可以考虑的标准.

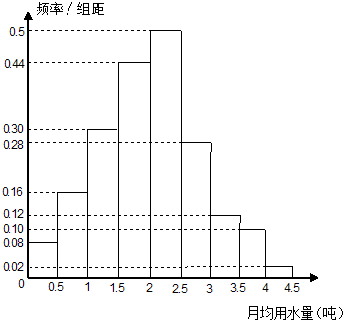 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,为此市政府首先采用抽样调查的方法获得了n位居民某年的月均用水量(单位:吨).根据所得的n个数据按照区间[0,0.5),[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5]进行分组,得到频率分布直方图如图
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,为此市政府首先采用抽样调查的方法获得了n位居民某年的月均用水量(单位:吨).根据所得的n个数据按照区间[0,0.5),[0.5,1),[1,1.5),[1.5,2),[2,2.5),[2.5,3),[3,3.5),[3.5,4),[4,4.5]进行分组,得到频率分布直方图如图 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准.为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量的标准.为了确定一个较为合理的标准,必须先了解全市居民日常用水量的分布情况.现采用抽样调查的方式,获得了n位居民某年的月均用水量(单位:t),样本统计结果如图表:

 位居民某年的月均用水量(单位:吨).根据所得的
位居民某年的月均用水量(单位:吨).根据所得的 进行分组,得到频率分布直方图如图
进行分组,得到频率分布直方图如图 和
和 内的人数;
内的人数; )
)