题目内容
在正三棱锥S-ABC中,M,N分别是SB,SC的中点.若面AMN⊥面SBC,则二面角S-BC-A的平面角的余弦值为________.

分析:如图,设D为BC中点,则 SD⊥BC,AD⊥SD,∠SDA二面角S-BC-A的平面角. 设底面边长为2,侧棱长为a,通过解三角形的方法,解得a=
 ,在△SAD中,由余弦定理求出∠SDA 的余弦值.
,在△SAD中,由余弦定理求出∠SDA 的余弦值.解答:
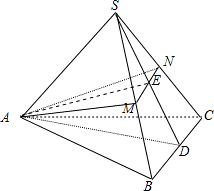 设D为BC中点,则 SD⊥BC,SD⊥MN,垂足为E,E为MN中点.又面AMN⊥面SBC,则 SE⊥面AMN,SE⊥AE.
设D为BC中点,则 SD⊥BC,SD⊥MN,垂足为E,E为MN中点.又面AMN⊥面SBC,则 SE⊥面AMN,SE⊥AE.又AD⊥SD,∴∠SDA二面角S-BC-A的平面角
设底面边长为2,侧棱长为a,在△SBC中,SD2=a2-1,SE2=
 SD2=
SD2=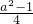 ,ME=
,ME= MN=
MN= .
.在△SAB中,由余弦定理,cos∠ASB=
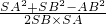 =
=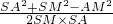 ,代入数据化简得
,代入数据化简得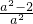 =
=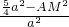 ,AM2=
,AM2=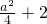 ,
,在△SAE中,由勾股定理,得出 SA2=AE2+SE2=AM2-ME2+E2,即a2=
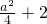 -
- +
+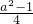 ,解得a2=3,a=
,解得a2=3,a=
在△SAD中,由余弦定理,cos∠SDA=
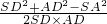 =
=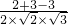 =
=
故答案为:
 .
.点评:本题考查二面角角的计算,线面垂直,面面垂直的定义,性质、判定,考查了空间想象能力、计算能力,分析解决问题能力.空间问题平面化是解决空间几何体问题最主要的思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
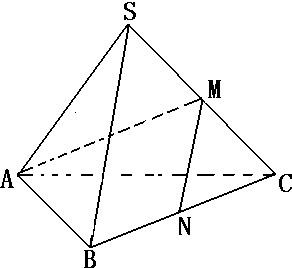 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
在正三棱锥S-ABC中,D是AB的中点,且SD与BC成45°角,则SD与底面ABC所成角的正弦为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|