题目内容
某圆拱桥的示意图如下图所示,该圆拱的跨度AB是36 m,拱高OP是6 m,在建造时,每隔3 m需用一个支柱支撑,求支柱A2P2的长.(精确到0.01 m)

[分析] 建系→求点的坐标→求圆的方程→求A2P2的长
[解析] 如图,以线段AB所在的直线为x轴,线段AB的中点O为坐标原点建立平面直角坐标系,那么点A,B,P的坐标分别为(-18,0),(18,0),(0,6).

设圆拱所在的圆的方程是x2+y2+Dx+Ey+F=0.
因为A,B,P在此圆上,故有
 故圆拱所在的圆的方程是x2+y2+48y-324=0.
故圆拱所在的圆的方程是x2+y2+48y-324=0.
将点P2的横坐标x=6代入上式,解得
y=-24+12![]() .
.
答:支柱A2P2的长约为12![]() -24.
-24.
[点评] 在实际问题中,遇到有关直线和圆的问题,通常建立坐标系,利用坐标法解决.建立适当的直角坐标系应遵循三点:①若曲线是轴对称图形,则可选它的对称轴为坐标轴;②常选特殊点作为直角坐标系的原点;尽量使已知点位于坐标轴上.建立适当的直角坐标系,会简化运算过程.

练习册系列答案
相关题目
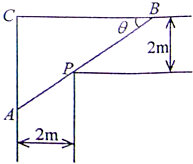 某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.
某直角走廊的示意图如图所示,其两边走廊的宽度均为2m.
