题目内容
已知函数 在
在 处取得极小值2.
处取得极小值2.
(1)求函数 的解析式;
的解析式;
(2)求函数 的极值;
的极值;
(3)设函数 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
(1)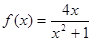
(2)当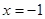 时,函数
时,函数 有极小值-2;当
有极小值-2;当 时,函数
时,函数 有极大值2
有极大值2
(3)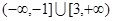
解析试题分析:(1)∵函数 在
在 处取得极小值2,
处取得极小值2,
∴ , ……1分
, ……1分
又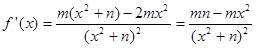 ,
,
∴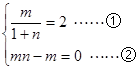
由②式得m=0或n=1,但m=0显然不合题意,
∴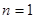 ,代入①式得m=4
,代入①式得m=4
∴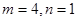 ……2分
……2分
经检验,当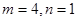 时,函数
时,函数 在
在 处取得极小值2, ……3分
处取得极小值2, ……3分
∴函数 的解析式为
的解析式为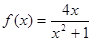 . ……4分
. ……4分
(2)∵函数 的定义域为
的定义域为 且由(1)有
且由(1)有 ,
,
令 ,解得:
,解得: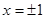 , ……5分
, ……5分
∴当x变化时, 的变化情况如下表: ……7分
的变化情况如下表: ……7分x 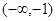
-1 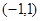
1 
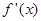
— 0 + 0 — 
天下通课时作业本系列答案
学业评价测评卷系列答案
同步检测卷系列答案
长沙中考系列答案
小学单元同步核心密卷系列答案
长江全能学案英语听力训练系列答案
随堂练习册课时练系列答案
中考整合集训系列答案
阳光课堂口算题系列答案
快乐每一天神算手天天练系列答案
 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围. 的导函数为
的导函数为 ,且
,且 。
。 的图象在x=0处的切线方程;
的图象在x=0处的切线方程; 为奇函数,a为常数。
为奇函数,a为常数。 的值;并证明
的值;并证明 在区间
在区间 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围. 。
。 在
在 上的单调性;
上的单调性; 在
在 上有极值,求
上有极值,求 的取值范围。
的取值范围。 ,其图象在点
,其图象在点 处的切线方程为
处的切线方程为
 的值;
的值; 的单调区间,并求出
的单调区间,并求出 (
( ).
). 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值; ,
,
 ,总有
,总有 ,求实数
,求实数
 的表达式,并判断
的表达式,并判断 时,恒有
时,恒有 求m的取值范围。
求m的取值范围。 和
和 组成数对(
组成数对( ,并构成函数
,并构成函数
 ,且
,且 的概率;
的概率; 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率.