题目内容
(本小题13分)
已知椭圆的焦点在 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线 的焦点,离心率
的焦点,离心率 ,过椭圆的右焦点
,过椭圆的右焦点 作不与坐标轴垂直的直线
作不与坐标轴垂直的直线 ,交椭圆于A、B两点.
,交椭圆于A、B两点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设点M(m,0)是线段OF上的一个动点,且 ,求
,求 取值范围;
取值范围;
(Ⅲ)设点C是点A关于x轴的对称点,在x轴上是否存在一个定点N,使得C、B、N 三点共线?若存在,求出定点N的坐标,若不存在,请说明理由.
【答案】
(1) 
(2) 
【解析】(Ⅰ)设椭圆方程为 ,由题意知
,由题意知 =1.
=1.
 ,
,
故椭圆方程为 .
.
(Ⅱ)由(Ⅰ)得 ,所以
,所以 . 设
. 设 的方程为
的方程为
 ,
,
代入 ,得
,得 ,
,
设 ,则
,则 ,
,
 ,
, ,
,
 ,
,
 ,
,

 ,
,
 ,
,

 ,
,
由 ,
,
 当
当 时, 有
时, 有 成立.
成立.
(Ⅲ)在 轴上存在定点
轴上存在定点 ,使得
,使得 、
、 、
、 三点共线.
三点共线.
依题意知 ,直线BC的方程为
,直线BC的方程为 ,
,
令y=0,则 ,
,
∵ 的方程为
的方程为 ,A、B在直线
,A、B在直线 上,
上,
∴
∴



∴在 轴上存在定点
轴上存在定点 ,使得
,使得 、
、 、
、 三点共线.
三点共线.
解法二:(Ⅰ)同解法一.(Ⅱ)由(Ⅰ)得 ,所以
,所以 .
.
设 的方程为
的方程为
 ,
,
代入 ,得
,得 ,
,
设 ,则
,则 ,
,
 ,
, ,
,
∵ ,∴
,∴ ,
,
∴ ,
,
∴ ,
,
 ,∴
,∴ ,
,
∴ ∵
∵ , ∴
, ∴ ,
,
∴ .
.
 当
当 时, , 有
时, , 有 成立.
成立.
(Ⅲ) 在 轴上存在定点
轴上存在定点 ,使得
,使得 、
、 、
、 三点共线.
三点共线.
设存在 ,使得
,使得 、
、 、
、 三点共线, 则
三点共线, 则 ∥
∥ ,
,
 ,
, ,
,
 ,
,
即 .
.

 ,
, .∴,存在
.∴,存在 ,使
,使 、
、 、
、 三点共线.
三点共线.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 。已知2010年生产饮料的设备折旧,维修等固定费用为3 万元,每生产1万件
。已知2010年生产饮料的设备折旧,维修等固定费用为3 万元,每生产1万件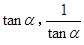 是关于
是关于 的方程
的方程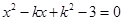 的两个实根,且
的两个实根,且 ,求
,求 的值
的值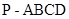 中,
中,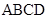 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面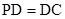 ,
,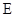 是
是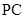 的中点,作
的中点,作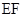 ⊥
⊥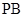 交
交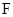 .
.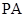 ∥平面
∥平面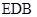 ;
;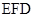 .
.