题目内容
对于向量 ,下列命题正确的个数是( )
,下列命题正确的个数是( )①若
 ,则
,则 ;
; ②
 ;
; ③若
 ,则
,则 ;
;④若
 是非零向量,且
是非零向量,且 ,则
,则 ;
; ⑤
 .
.A.1个
B.2个
C.3个
D.4个
【答案】分析:由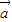 •
•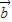 =0?
=0?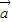 ⊥
⊥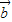 ,及|
,及|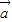 +
+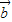 |=
|=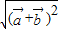 可对①④作出判断;由
可对①④作出判断;由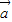 •
•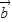 =|
=|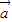 |•|
|•|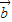 |cos<
|cos<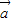 ,
,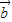 >可对②作出判断;根据零向量与任意向量共线可对③作出判断,根据向量的减法法则可对⑤作出判断,综合可得答案.
>可对②作出判断;根据零向量与任意向量共线可对③作出判断,根据向量的减法法则可对⑤作出判断,综合可得答案.
解答:解:①若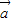 •
•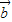 =0,则若
=0,则若 ⊥
⊥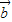 ,未必|
,未必|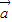 |=0,|
|=0,|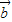 |=0,所以①错误;
|=0,所以①错误;
②(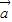 •
•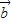 )2=(|
)2=(|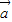 |•|
|•|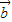 |cos<
|cos< ,
,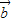 >)2=
>)2=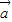 2•
2•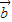 2cos2<
2cos2<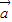 ,
,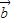 >,cos<
>,cos<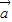 ,
,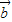 >未必为1,所以②错误;
>未必为1,所以②错误;
③取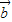 =
=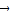 ,则对于任意向量
,则对于任意向量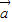 ,
,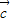 都有
都有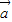 ∥
∥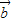 ,
,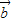 ∥
∥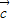 ,但得不到
,但得不到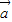 ∥
∥ ,所以③错误;
,所以③错误;
④若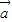 、
、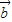 是非零向量,且
是非零向量,且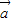 ⊥
⊥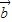 ,则
,则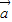 •
•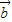 =0,那么|
=0,那么|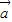 +
+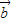 |=
|=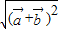 =
=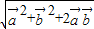 =
=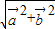 ,
,
同理|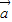 -
-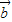 |=
|=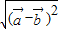 =
=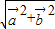 ,所以|
,所以|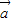 +
+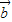 |=|
|=|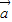 -
-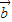 |成立,即④正确.
|成立,即④正确.
⑤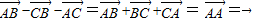 ,故⑤正确
,故⑤正确
故正确的有2个
故选B
点评:本题主要考查相等向量、相反向量的概念,以及向量的数量积公式、模长公式,及向量垂直的充要条件等有关知识,属于中档题.
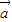 •
•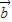 =0?
=0?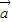 ⊥
⊥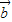 ,及|
,及|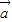 +
+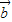 |=
|=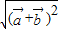 可对①④作出判断;由
可对①④作出判断;由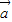 •
•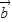 =|
=|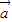 |•|
|•|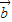 |cos<
|cos<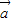 ,
,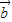 >可对②作出判断;根据零向量与任意向量共线可对③作出判断,根据向量的减法法则可对⑤作出判断,综合可得答案.
>可对②作出判断;根据零向量与任意向量共线可对③作出判断,根据向量的减法法则可对⑤作出判断,综合可得答案.解答:解:①若
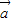 •
•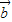 =0,则若
=0,则若 ⊥
⊥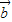 ,未必|
,未必|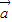 |=0,|
|=0,|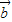 |=0,所以①错误;
|=0,所以①错误;②(
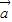 •
•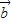 )2=(|
)2=(|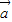 |•|
|•|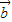 |cos<
|cos< ,
,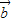 >)2=
>)2=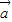 2•
2•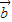 2cos2<
2cos2<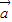 ,
,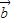 >,cos<
>,cos<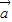 ,
,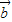 >未必为1,所以②错误;
>未必为1,所以②错误;③取
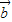 =
=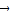 ,则对于任意向量
,则对于任意向量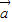 ,
,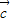 都有
都有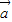 ∥
∥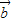 ,
,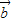 ∥
∥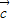 ,但得不到
,但得不到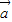 ∥
∥ ,所以③错误;
,所以③错误;④若
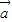 、
、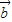 是非零向量,且
是非零向量,且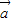 ⊥
⊥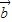 ,则
,则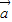 •
•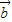 =0,那么|
=0,那么|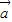 +
+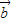 |=
|=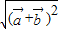 =
=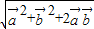 =
=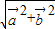 ,
,同理|
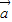 -
-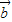 |=
|=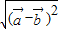 =
=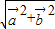 ,所以|
,所以|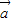 +
+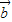 |=|
|=|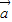 -
-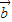 |成立,即④正确.
|成立,即④正确.⑤
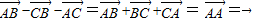 ,故⑤正确
,故⑤正确故正确的有2个
故选B
点评:本题主要考查相等向量、相反向量的概念,以及向量的数量积公式、模长公式,及向量垂直的充要条件等有关知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于非零向量
、
,下列命题中正确的是( )
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
 、
、 ,下列命题中正确的是( )
,下列命题中正确的是( ) 或
或
 ∥
∥ ⇒
⇒ 在
在 上的正射影的数量为
上的正射影的数量为


 、
、 ,下列命题中正确的是( )
,下列命题中正确的是( ) 或
或
 ∥
∥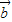 ⇒
⇒ 在
在 上的正射影的数量为
上的正射影的数量为

