题目内容
函数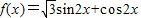 ,给出下列三个命题:
,给出下列三个命题:①函数
 上是减函数;
上是减函数;②直线
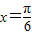 是函数f(x)的图象的一条对轴称;
是函数f(x)的图象的一条对轴称;③函数f(x)的图象可以由函数y=2sin2x的图象向右平移
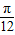 而得到.
而得到.其中正确的是 .(写出所有正确结论的编号)
【答案】分析:利用两角和的正弦函数化简函数的表达式,
①通过函数的单调减区间,直接判断,函数 上是减函数,是否正确;
上是减函数,是否正确;
②利用 ,函数是否取得最值,判断直线
,函数是否取得最值,判断直线 是函数f(x)的图象的一条对轴称是否正确;
是函数f(x)的图象的一条对轴称是否正确;
③直接按照函数f(x)的图象可以由函数y=2sin2x的图象向右平移 而得到求出函数的解析式,即可判断正误.
而得到求出函数的解析式,即可判断正误.
解答:解:函数 =2sin(2x+
=2sin(2x+ ),
),
①因为 k∈Z,解得
k∈Z,解得 时函数单调递减,
时函数单调递减,
令k=0, ,函数
,函数 上是减函数;所以①正确.
上是减函数;所以①正确.
②当 时,是函数f(x)=2sin(2×
时,是函数f(x)=2sin(2× +
+ )=2,
)=2,
此时函数取得最大值,所以 是函数的图象的一条对轴称;正确.
是函数的图象的一条对轴称;正确.
③函数f(x)的图象可以由函数y=2sin2x的图象向右平移 而得到f(x)=2sin(2x-
而得到f(x)=2sin(2x- ),
),
不正确.
故答案为:①②.
点评:本题考查两角和的正弦函数的应用,函数的单调性、对称性、图象的平移,考查基本知识的灵活运用.
①通过函数的单调减区间,直接判断,函数
 上是减函数,是否正确;
上是减函数,是否正确;②利用
 ,函数是否取得最值,判断直线
,函数是否取得最值,判断直线 是函数f(x)的图象的一条对轴称是否正确;
是函数f(x)的图象的一条对轴称是否正确;③直接按照函数f(x)的图象可以由函数y=2sin2x的图象向右平移
 而得到求出函数的解析式,即可判断正误.
而得到求出函数的解析式,即可判断正误.解答:解:函数
 =2sin(2x+
=2sin(2x+ ),
),①因为
 k∈Z,解得
k∈Z,解得 时函数单调递减,
时函数单调递减,令k=0,
 ,函数
,函数 上是减函数;所以①正确.
上是减函数;所以①正确.②当
 时,是函数f(x)=2sin(2×
时,是函数f(x)=2sin(2× +
+ )=2,
)=2,此时函数取得最大值,所以
 是函数的图象的一条对轴称;正确.
是函数的图象的一条对轴称;正确.③函数f(x)的图象可以由函数y=2sin2x的图象向右平移
 而得到f(x)=2sin(2x-
而得到f(x)=2sin(2x- ),
),不正确.
故答案为:①②.
点评:本题考查两角和的正弦函数的应用,函数的单调性、对称性、图象的平移,考查基本知识的灵活运用.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ,给出下列三个命题:
,给出下列三个命题: 上是减函数;
上是减函数; 是函数f(x)的图象的一条对称轴;
是函数f(x)的图象的一条对称轴; 的图象向左平移
的图象向左平移 而得到.
而得到.