题目内容
在一个圆锥体的培养房内培养了40只蜜蜂,准备进行某种实验,过圆锥高的中点有一个不计厚度且平行于圆锥底面的平面把培养房分成两个实验区,其中小锥体叫第一实验区,圆台体叫第二实验区,且两个实验区是互通的. 假设蜜蜂落入培养房内任何位置是等可能的,且蜜蜂落入哪个位置相互之间是不受影响的.
(1)求蜜蜂落入第二实验区的概率;
(2)若其中有10只蜜蜂被染上了红色,求恰有一只红色蜜蜂落入第二实验区的概率;
(3)记![]() 为落入第一实验区的蜜蜂数,求随机变量
为落入第一实验区的蜜蜂数,求随机变量![]() 的数学期望.
的数学期望.
(本小题主要考查几何概型、二项分布、数学期望等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)
解:(1)记“蜜蜂落入第一实验区”为事件![]() ,
,
“蜜蜂落入第二实验区”为事件![]() .………1分
.………1分
依题意,![]()
 ……………3分
……………3分
∴ ![]()
∴ 蜜蜂落入第二实验区的概率为![]() . …………4分
. …………4分
(2)记“恰有一只红色蜜蜂落入第二实验区”为事件![]() ,
,
则 …………5分
![]()
∴ 恰有一只红色蜜蜂落入第二实验区的概率![]() . …………8分
. …………8分
(3)因为蜜蜂落入培养房内任何位置是等可能的,
且蜜蜂落入哪个位置相互之间是不受影响的,
所以变量![]() 满足二项分布,即
满足二项分布,即![]() ~
~![]() ……………10分
……………10分
∴随机变量X的数学期望![]() =40×
=40×![]() =5 ……………12分
=5 ……………12分

练习册系列答案
相关题目
 为落入第一实验区的蜜蜂数,求随机变量
为落入第一实验区的蜜蜂数,求随机变量 。
。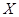 为落入第一实验区的蜜蜂数,求随机变量
为落入第一实验区的蜜蜂数,求随机变量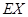 。
。