题目内容

设a＞0，b＞0，2c＞a+b，求证：c-
c2-ab
＜a＜c+
c2-ab
．
分析：可采用分析法，要证原不等式成立，需证：-
c2-ab
＜a-c＜
c2-ab
，即证：（a-c）2＜c2-ab，展开整理，结合已知中的条件a＞0，b＞0，2c＞a+b，即可证得结论．
解答：证明：要证c-
c2-ab
＜a＜c+
c2-ab
，
即证：-
c2-ab
＜a-c＜
c2-ab
，
即证：（a-c）2＜c2-ab，
即证：a2-2ac＜-ab，
即证：a2+ab＜2ac．
∵a＞0，
也就是证：a+b＜2c，而此不等式为已知条件，显然成立．
故不等式c-
c2-ab
＜a＜c+
c2-ab
成立．
点评：本题考查不等式的证明，着重考查分析法，考查转化思想与推理能力，属于中档题．
练习册系列答案
相关题目
设a＞0，b＞0，若1是a与b的等比中项，则
1
a
+
1
b
的最小值为（　　）

对于集合M、N，定义M－N＝{x|x∈M且x∉N}，M⊕N＝(M－N)∪(N－M)，设A＝{y|y＝3x，x∈R}，B＝{y|y＝－(x－1)2＋2，x∈R}，则A⊕B等于  (　　)

A．[0,2)                                                 B．(0,2]

C．(－∞，0]∪(2，＋∞)                                  D．(－∞，0)∪[2，＋∞)

 

设a>0，b>0，a+b=1，则ab的最大值为 　　　　　　　　　　　　　　　（　　）

A．2  　　 B．　　　  C．　4   　　　　　     D．

 
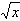已知函数f（x）=，g（x）=alnx，a∈R。
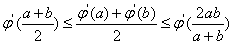（1）若曲线y=f（x）与曲线y=g（x）相交，且在交点处有共同的切线，求a的值和该切线方程；
（2）设函数h（x）=f（x）-g（x），当h（x）存在最小值时，求其最小值φ（a）的解析式；
（3）对（2）中的φ（a）和任意的a>0，b>0，证明：。

设a>0，b>0，a+b=1，则ab的最大值为 　　　　　　　　　　　　　　　（　　）

A．2  　　 B．　　　  C．　4   　　　　　     D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网