题目内容

设f（x）是定义在（-∞，+∞）上的奇函数，且在区间（0，+∞）上单调递增，若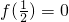 $数学公式$ ，三角形的内角A满足f（cosA）＜0，则A的取值范围是________．

$\text{[math]}$
分析：根据函数在R上的奇偶性和在区间（0，+∞）上的单调性可以判断f（x）在区间（-∞，0）的单调性再分角A是锐角，直角还是钝角三种情况讨论，cosA的正负，利用f（x）的单调性解不等式．
解答：∵f（x）是定义在（-∞，+∞）上的奇函数，且在区间（0，+∞）上单调递增，
∴f（x）在区间（-∞，0）上也单调递增．
∵ $\text{[math]}$ ，∴ $\text{[math]}$ ，
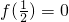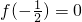当A为锐角时，cosA＞0，∴不等式f（cosA）＜0变形为f（cosA）＜f（ $\text{[math]}$ ），0＜cosA＜ $\text{[math]}$ ， $\text{[math]}$ ＜A＜ $\text{[math]}$
当A为直角时，cosA=0，而奇函数满足f（0）=0，∴A为直角不成立．
当A为钝角时，cosA＜0，∴不等式f（cosA）＜0变形为f（cosA）＜f（- $\text{[math]}$ ），＜cosA＜- $\text{[math]}$ ， $\text{[math]}$ ＜A＜π
综上，A的取值范围为 $\text{[math]}$
故答案为 $\text{[math]}$
点评：本题主要考查了综合运用函数的单调性和奇偶性解含函数符号的不等式，易错点是只考虑函数在（0，+∞）的单调性，没有考虑（-∞，0）的单调性．