题目内容
若数列{an}是等比数列,则下列命题正确的个数是( )①{
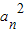 },{a2n}是等比数列
},{a2n}是等比数列 ②{lgan}是等差数列
③{
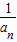 },{|an|}是等比数列
},{|an|}是等比数列 ④{can},{an±k}(k≠0)是等比数列.
A.4
B.3
C.2
D.1
【答案】分析:根据等比数列的定义,可判断{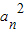 }是一个以a12为首项,以q2为公比的等比数列,{a2n}是一个以a2为首项,以q2为公比的等比数列,{
}是一个以a12为首项,以q2为公比的等比数列,{a2n}是一个以a2为首项,以q2为公比的等比数列,{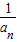 }是一个以
}是一个以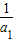 为首项,以
为首项,以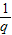 为公比的等比数列,{|an|}是一个以|a1|为首项,以|q|为公比的等比数列,而其它不一定是等比数列
为公比的等比数列,{|an|}是一个以|a1|为首项,以|q|为公比的等比数列,而其它不一定是等比数列
解答:解:若数列{an}是等比数列,且首项为a1,公比为q,则an=a1•qn-1,
则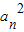 =a12•q2(n-1),这是一个以a12为首项,以q2为公比的等比数列,a2n=a1•q2n-1=a1q•q2(n-1)=a2•q2(n-1),这是一个以a2为首项,以q2为公比的等比数列,故①正确;
=a12•q2(n-1),这是一个以a12为首项,以q2为公比的等比数列,a2n=a1•q2n-1=a1q•q2(n-1)=a2•q2(n-1),这是一个以a2为首项,以q2为公比的等比数列,故①正确;
当q<0时,数列{an}存在负项,此时lgan无意义,故②错误;
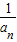 =
=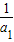 •
•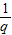 (n-1),这是一个以
(n-1),这是一个以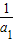 为首项,以
为首项,以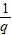 为公比的等比数列,|an|=|a1|•|q|n-1,这是一个以|a1|为首项,以|q|为公比的等比数列,故③正确;
为公比的等比数列,|an|=|a1|•|q|n-1,这是一个以|a1|为首项,以|q|为公比的等比数列,故③正确;
当c=0时,can=0,此时数列{can}不是等比数列,当k=-a1时,a1+k=0,此时{an+k}不是等比数列,当k=a1时,a1-k=0,此时{an-k}不是等比数列,故④错误
故选C
点评:本题考查的知识点是等比数列,熟练掌握等比数列的定义是解答的关键.
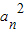 }是一个以a12为首项,以q2为公比的等比数列,{a2n}是一个以a2为首项,以q2为公比的等比数列,{
}是一个以a12为首项,以q2为公比的等比数列,{a2n}是一个以a2为首项,以q2为公比的等比数列,{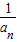 }是一个以
}是一个以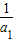 为首项,以
为首项,以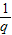 为公比的等比数列,{|an|}是一个以|a1|为首项,以|q|为公比的等比数列,而其它不一定是等比数列
为公比的等比数列,{|an|}是一个以|a1|为首项,以|q|为公比的等比数列,而其它不一定是等比数列解答:解:若数列{an}是等比数列,且首项为a1,公比为q,则an=a1•qn-1,
则
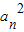 =a12•q2(n-1),这是一个以a12为首项,以q2为公比的等比数列,a2n=a1•q2n-1=a1q•q2(n-1)=a2•q2(n-1),这是一个以a2为首项,以q2为公比的等比数列,故①正确;
=a12•q2(n-1),这是一个以a12为首项,以q2为公比的等比数列,a2n=a1•q2n-1=a1q•q2(n-1)=a2•q2(n-1),这是一个以a2为首项,以q2为公比的等比数列,故①正确;当q<0时,数列{an}存在负项,此时lgan无意义,故②错误;
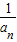 =
=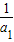 •
•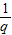 (n-1),这是一个以
(n-1),这是一个以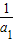 为首项,以
为首项,以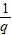 为公比的等比数列,|an|=|a1|•|q|n-1,这是一个以|a1|为首项,以|q|为公比的等比数列,故③正确;
为公比的等比数列,|an|=|a1|•|q|n-1,这是一个以|a1|为首项,以|q|为公比的等比数列,故③正确;当c=0时,can=0,此时数列{can}不是等比数列,当k=-a1时,a1+k=0,此时{an+k}不是等比数列,当k=a1时,a1-k=0,此时{an-k}不是等比数列,故④错误
故选C
点评:本题考查的知识点是等比数列,熟练掌握等比数列的定义是解答的关键.

练习册系列答案
相关题目
 给出下列四个命题:
给出下列四个命题: ;
; ,则α+β=1是A、B、C三点共线的充要条件;
,则α+β=1是A、B、C三点共线的充要条件; (p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;
(p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;

 0,b
0,b =p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.
=p(p为正常数,n∈N*),则称{an}为“等方比数列”.若数列{an}是等方比数列则数列{an}必是等比数列.