题目内容
(12分)已知椭圆![]() ,抛物线
,抛物线![]() ,且
,且![]() 、
、![]() 的公共弦
的公共弦![]() 过椭圆
过椭圆![]() 的右焦点 .
的右焦点 .
(1)当![]() 轴时,求
轴时,求![]() 、
、![]() 的值,并判断抛物线
的值,并判断抛物线![]() 的焦点是否在直线
的焦点是否在直线![]() 上;
上;
(2)若![]() 且抛物线
且抛物线![]() 的焦点在直线
的焦点在直线![]() 上,求
上,求![]() 的值及直线
的值及直线![]() 的方程.
的方程.

解析:(1)当![]() 轴时,点
轴时,点![]() 、
、![]() 关于
关于![]() 轴对称,所以
轴对称,所以![]() 直线
直线![]() 的方程为
的方程为![]() 从而点
从而点![]() 的坐标为
的坐标为![]() 或
或![]() 。因为点
。因为点![]() 在抛物线上,所以
在抛物线上,所以![]() ,即
,即![]() 。此时
。此时![]() 的焦点坐标为
的焦点坐标为![]() ,该焦点不在直线
,该焦点不在直线![]() 上。
上。
(2)![]() 直线
直线![]() 过点
过点![]() 及抛物线的焦点
及抛物线的焦点![]() ,
,![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() ,由
,由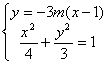 ,消去
,消去![]() 得
得![]() ,设
,设![]() 、
、![]() ,则
,则![]() ,又由
,又由 ,消去
,消去![]() 得
得
![]() ,则
,则![]() ;
;![]() 有
有![]() ,解得
,解得![]() ;
;![]()
![]() 的方程为
的方程为![]() 。
。

练习册系列答案
相关题目
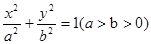 的左、右顶点的坐标分别为
的左、右顶点的坐标分别为 ,
, ,离心率
,离心率 。
。 ,
, ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两点,证明直线
两点,证明直线 与直线
与直线 的交点在直线
的交点在直线 上。
上。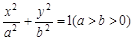 的离心率为
的离心率为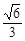 ,椭圆C上任意一点到椭圆两焦点的距离和为6.
,椭圆C上任意一点到椭圆两焦点的距离和为6.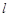 :
: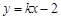 与椭圆C交于A,B两点,点P(0,1),且
与椭圆C交于A,B两点,点P(0,1),且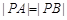 ,求直线
,求直线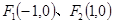 ,
, 为椭圆上一点,且
为椭圆上一点,且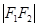 是
是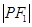 与
与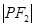 的等差中项.
的等差中项.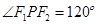 ,求
,求 的面积.
的面积.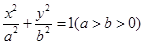 的离心率
的离心率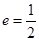 ,且原点
,且原点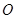 到直线
到直线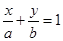 的距离为
的距离为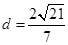 .
.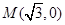 作直线与椭圆C交于
作直线与椭圆C交于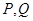 两点,求
两点,求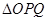 面积的最大值.
面积的最大值.